Musing 121: Decomposing Elements of Problem Solving: What "Math" Does RL Teach?
Fascinating paper out of Harvard and Kempner
Today’s paper: Decomposing Elements of Problem Solving: What "Math" Does RL Teach? Qin et al. 28 May 2025. https://arxiv.org/pdf/2505.22756
In recent months, large language models (LLMs) have made rapid strides in mathematical reasoning, with much of the progress attributed to reinforcement learning (RL) approaches such as Group Relative Policy Optimization (GRPO). These advances have typically been assessed using a single metric: Pass@1 accuracy, which measures the proportion of problems correctly solved on the first try. This approach reflects a broader pattern in cognitive science of favoring simple, aggregate metrics (like standardized test scores or IQ) to evaluate complex abilities. Such metrics remain popular in part because they are straightforward to interpret and allow for easy comparisons.
However, relying solely on Pass@1 accuracy presents two significant drawbacks:
First, it is overly simplistic and fails to illuminate the specific reasoning skills being developed or the types of errors models make. It offers little insight into whether RL improves aspects like planning, computation, error-checking, or simply reinforces known patterns.
Second, Pass@1 is based on greedy decoding, while real-world applications often depend on stochastic sampling techniques to enhance output diversity and robustness.
A deeper understanding of RL’s impact on reasoning demands evaluation frameworks that go beyond single accuracy scores to examine how models engage in the problem-solving process. This is what today’s paper takes a look at.
The authors adopt a finer-grained evaluation framework aimed at understanding two key questions:
(i) are the improvements from GRPO uniform across problems?, and
(ii) what specific aspects of reasoning does GRPO improve?
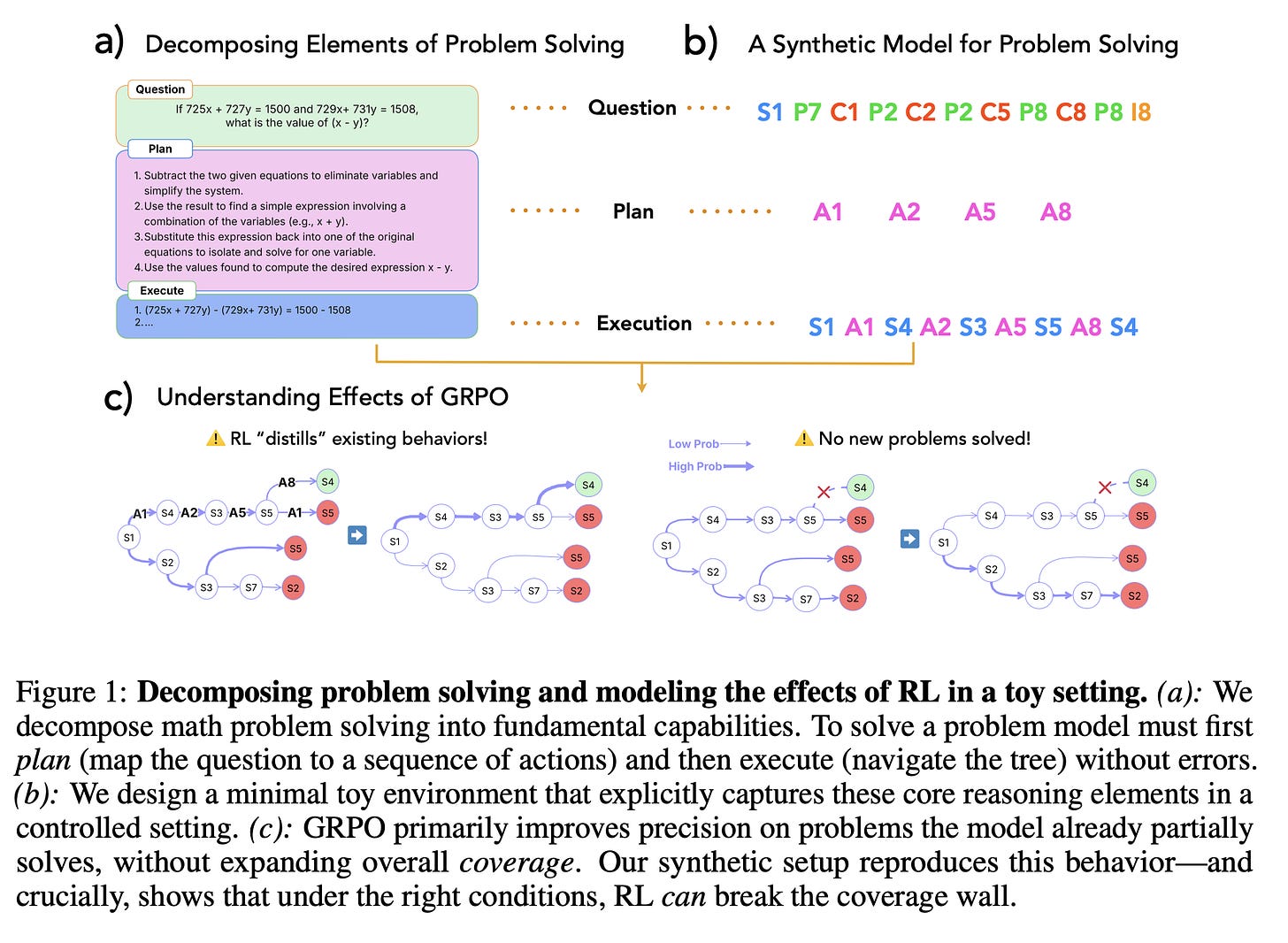
The authors’ perspective decomposes reasoning into three core skills (Fig. 1a above): Plan (mapping the question to a sequence of actions indicating where to go in the tree, Execute (carrying out those steps correctly by performing the navigation), and Verify (detecting and correcting errors). Using this lens, they find that even small models often plan well but frequently fail in execution, making logical and factual errors. GRPO, the authors show, primarily strengthens execution.
To better isolate and understand RL’s effects, the authors construct a minimal, synthetic setting that abstracts mathematical problem solving (Fig. 1b). Here, the model needs to map the question to a sequence of actions (i.e., plan) and execute the sequence of actions to provide the correct answer. This controlled environment closely mirrors the authors’ proposed framework, while allowing control over the underlying data generation process.
Ultimately, the study provides insights into RL’s role in enhancing LLM reasoning. The contributions are:
• Reasoning Decomposition: The proposed framework decomposes math problem solving into three capabilities: planning, execution, and verification.
• Empirical Analysis of RL: In the proposed decomposition, the authors show that GRPO primarily improves execution on known problems, leading to a temperature distillation effect. However, GRPO fails to help model solve previously unsolved problems, revealing a coverage wall.
• Synthetic Validation: The authors construct a minimal synthetic task that closely reflects the fundamental elements of problem solving and replicates empirical findings, and reveal some data properties under which RL can overcome the coverage wall.
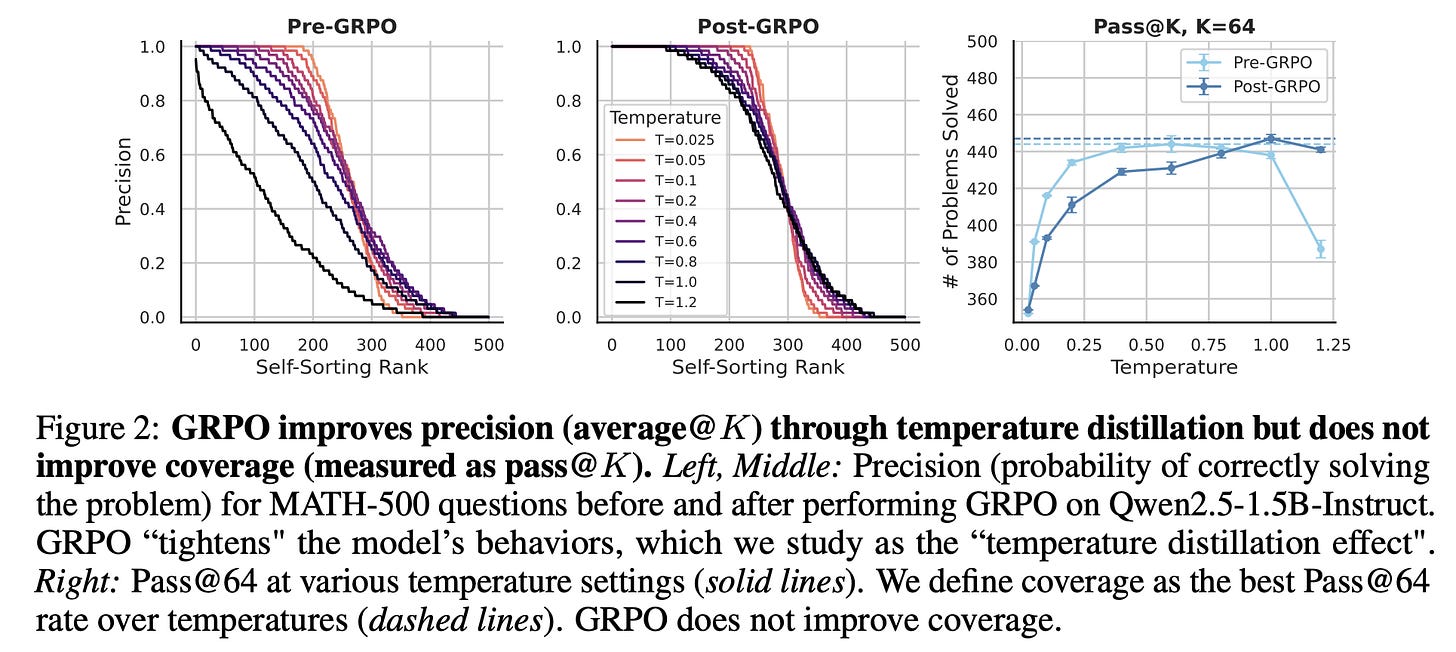
The authors begin the core content of the paper by ‘breaking down the accuracy metric’ and arguing that a single accuracy score is insufficient to comprehensively evaluate model performance. With RL models surpassing 70% accuracy on hard math benchmarks, it’s tempting to conclude they are capable reasoners. However, this metric can be misleading. First, real-world deployments rarely operate at a fixed temperature; robust reasoning should generalize across sampling regimes. Second, many use cases rely on test-time scaling strategies like Best-of-N or Majority Voting [45], which Pass@K (especially with K = 1 at a fixed temperature) is insensitive to. As a result, we have limited insights into what capabilities RL actually enhances. In conducting an experiment (Figure 2 below), the authors find that before GRPO, temperature heavily affects performance: higher temperatures reduce precision on easy problems but slightly improve success on harder ones, reflecting more exploratory behavior.
After GRPO, this temperature sensitivity largely disappears—precision curves flatten across all temperatures. The authors refer to this robustness to sampling temperature as the temperature distillation effect. This phenomenon is only partially reflected using Pass@K, which captures model behavior at a fixed temperature and overlooks full distribution change across the problem difficulty spectrum.
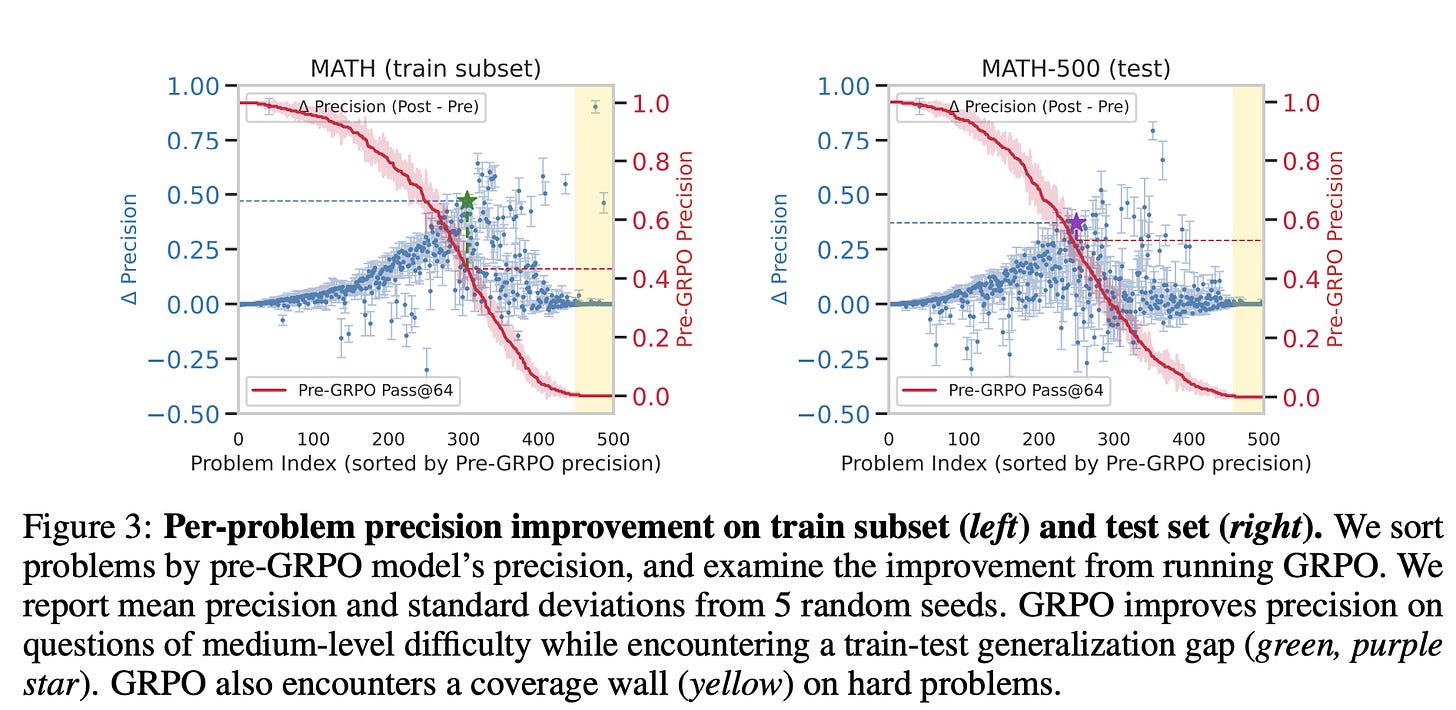
The authors then show that moving to a more fine-grained metric reveals that the predominant effect of RL can be understood as temperature distillation (an increase in precision,) without improving coverage. A central question they examine is whether RL enables the model to solve problems it previously could not (they show that GRPO doesn’t). To analyze the fine-grained effects of GRPO on problem solvability, a matched-problem analysis is conducted by sorting problems according to their pre-GRPO precision and comparing precision values before and after GRPO for each. Figure 3 (left) presents results on a subset of the training set, while Figure 3 (right) shows corresponding outcomes on the test set.
In the training set (Figure 3, left), GRPO produces minimal gains on problems that the model already solves with high precision, due to saturation effects. The most substantial improvements occur for problems with medium initial precision. Specifically, the green star marks a cluster of problems around 40% pre-GRPO precision that see the largest absolute improvement—approximately 45%. In contrast, on the test set (Figure 3, right), the peak improvement shifts to problems with slightly higher initial precision—around 60%—highlighted in purple. These are problems the model could already solve using majority voting, and the gains here are smaller, around 35%.
Beyond this medium-precision region, gains taper off quickly. On the training subset, GRPO unlocks only two previously unsolved problems. Importantly, this progress does not transfer: on the test set, GRPO fails to solve any new problems, illustrating what is referred to as the coverage wall.
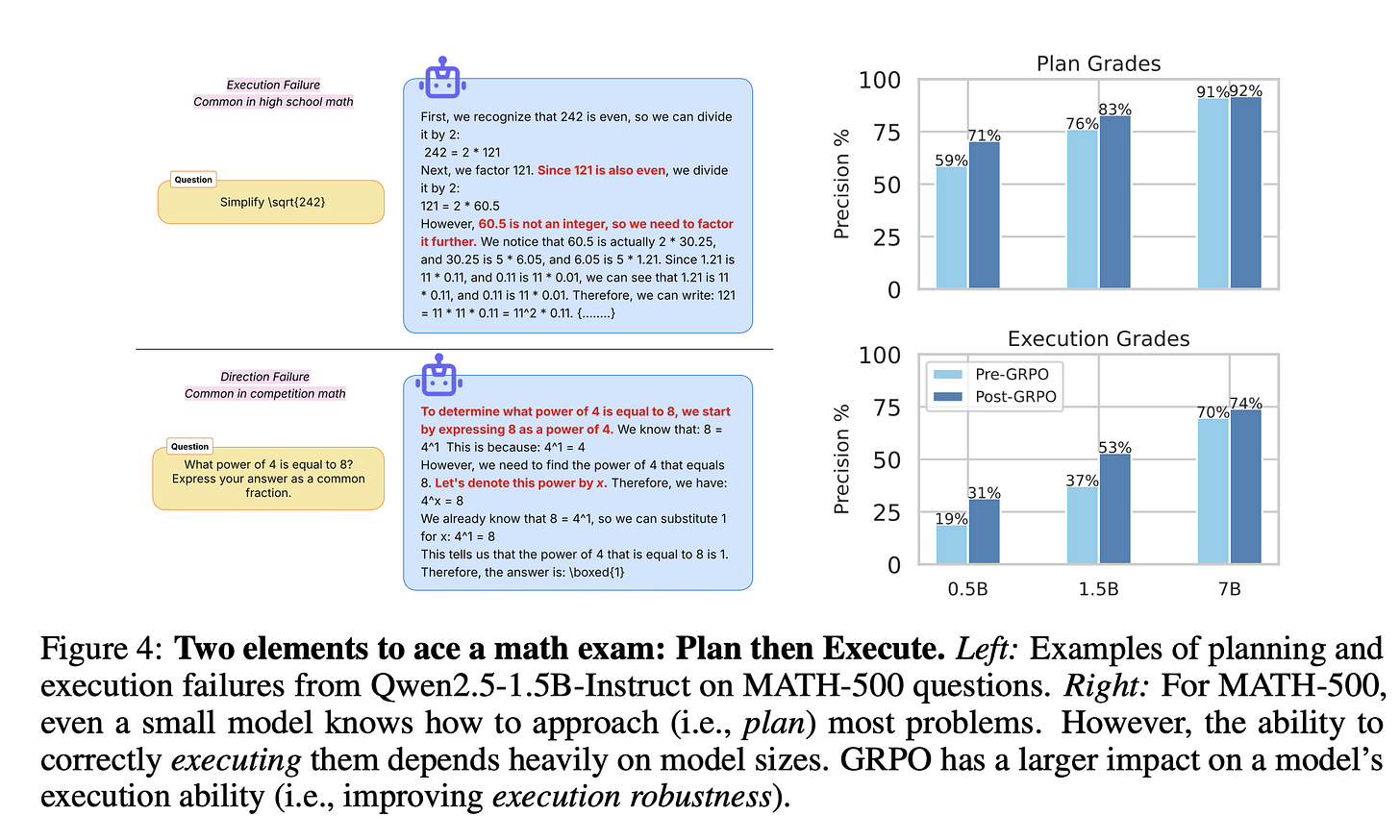
The authors conduct a range of experiments, but I’ll just summarize a couple more here. First, they find that even small models often know how to plan most problems, but the execution of the plan can depend heavily on the model sizes:
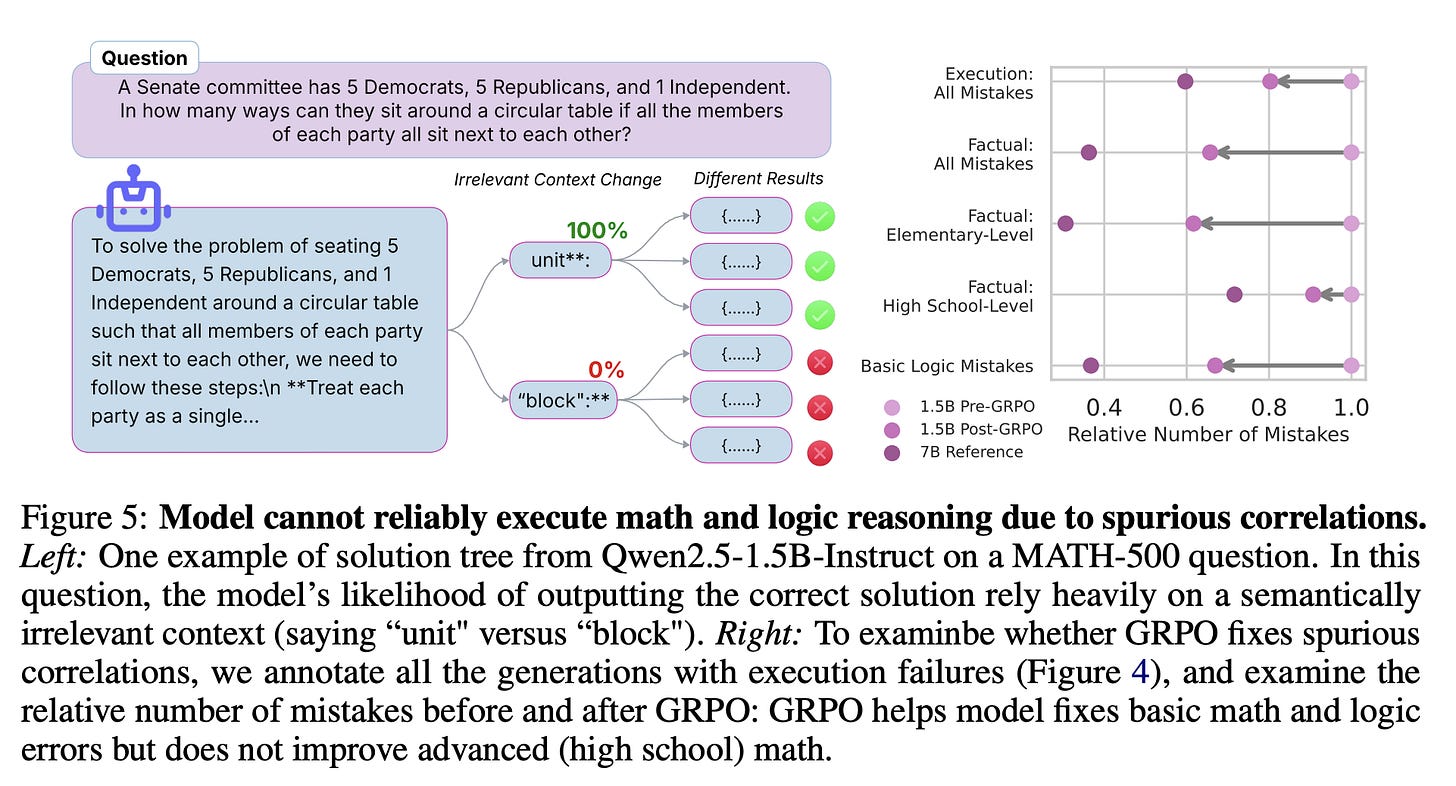
But why do models often fail to execute solution steps correctly? Understanding these failures would shed light on the limits of their reasoning capabilities. To this end, the authors implement a visualization tool that convert model’s solution roll out into a solution tree, branching whenever generations diverge. Using this visualization tool, they inspect model’s solution tree across 30 different MATH-500 questions. A consistent pattern emerges: models apply mathematical and logical steps probabilistically, often influenced by spurious correlations such as formatting or phrasing in the chain-of-thought.
For instance, Fig. 5 (left) shows Qwen2.5-1.5B’s generation tree on a problem where solutions diverge based on whether the word “unit" or “block" is used. Although the wording choice is semantically irrelevant, it significantly affects whether the model produces a correct solution. This suggests that execution accuracy is driven more by superficial patterns in the training data than by robust reasoning. Despite strong benchmark scores (1.5B achieves ≥ 50% on high shcool MATH-500, ≥ 70% on grade-school GSM8K)—these models still make basic factual and logical errors—many of which would be obvious to elementary school students. The authors further hypothesize that temperature distillation mitigates these issues by encouraging solution traces that are less sensitive to such spurious cues, improving consistency across generations.
Concluding this musing, the authors propose a decomposition of mathematical reasoning in LLMs into three core capabilities: planning, execution, and verification. Using this framework, they conduct a in-depth analysis of reinforcement learning (specifically GRPO) and find that it primarily enhances execution robustness, but does not improve planning or expand the set of problems the model can solve (coverage). However, there are some limitations. The focus is on small-scale models and publicly available datasets, which as such, cannot eliminate the possibility that larger models trained on more extensive data may exhibit emergent behaviors. It remains plausible that improvements in curriculum design or the use of broader RL datasets could enhance planning capabilities and expand coverage. Additionally, while the synthetic environment helps uncover key mechanisms, its limited state space makes it more vulnerable to brute-force sampling strategies, which may overstate the ease of achieving generalization compared to real-world scenarios.
Nonetheless, the proposed decomposition serves as a useful conceptual tool for analyzing reasoning-specific behavior. The authors aim for this approach to inspire future research that goes beyond aggregate accuracy metrics and instead examines how distinct reasoning skills emerge, interact, and evolve across different training regimes and data sources.