Musing 126: Does Math Reasoning Improve General LLM Capabilities?

Excellent multi-team paper on a hot topic from CMU, UPenn, UW, M-A-P, Hong Kong Polytechnic

Today’s paper: Does Math Reasoning Improve General LLM Capabilities? Understanding Transferability of LLM Reasoning. Huan et al. 1 July, 2025. https://arxiv.org/pdf/2507.00432

Mathematical reasoning has emerged as a showcase for the rapid progress of large language models, which are now frequently exceeding human-level performance on benchmarks such as MATH and AIME. However, despite these frequent improvements on math leaderboards, it remains important to ask whether the observed gains signify true general problem-solving ability or simply reflect narrow overfitting to benchmark tasks. A continual stream of models fine-tuned for reasoning is pushing the state of the art forward almost weekly, with some surpassing average expert-level performance.

The appeal of mathematical benchmarks is clear: the problems are well-defined, the solutions unambiguous, and the evaluations straightforward, often requiring just a single numeric or symbolic answer. This makes math a favored proxy for assessing LLM reasoning capabilities. In response, the research community has developed increasingly sophisticated training techniques aimed at optimizing models specifically for mathematical tasks.

This emphasis on math is not without merit. Since mathematics is often viewed as the foundational language of science, empowering machines to reason accurately in this domain aligns with long-term goals such as automated scientific discovery. Still, there are limitations. Most real-world applications—including user interaction, dialogue systems, and instruction-following—demand a much broader range of skills, including linguistic fluency and commonsense reasoning, that pure mathematical training does not adequately address.

In today’s paper, the authors raise a natural question: Do improved math reasoning abilities transfer to general LLM capabilities? To investigate, they evaluate over 20 representative open-weight reasoning models, all of which exhibit impressive performance on recent math benchmarks across a suite of other reasoning and non-reasoning tasks. They then do a controlled study using two important learning techniques: they fine-tune Qwen3-14B on a high-quality math dataset derived from MATH and DeepScaler. For supervised fine-tuning (SFT), they construct targets via rejection sampling using Qwen3-32B, keeping only teacher responses that yield correct final answers. For reinforcement learning (RL), they apply a standard GRPO (Shao et al., 2024) setup using answer correctness as the reward.

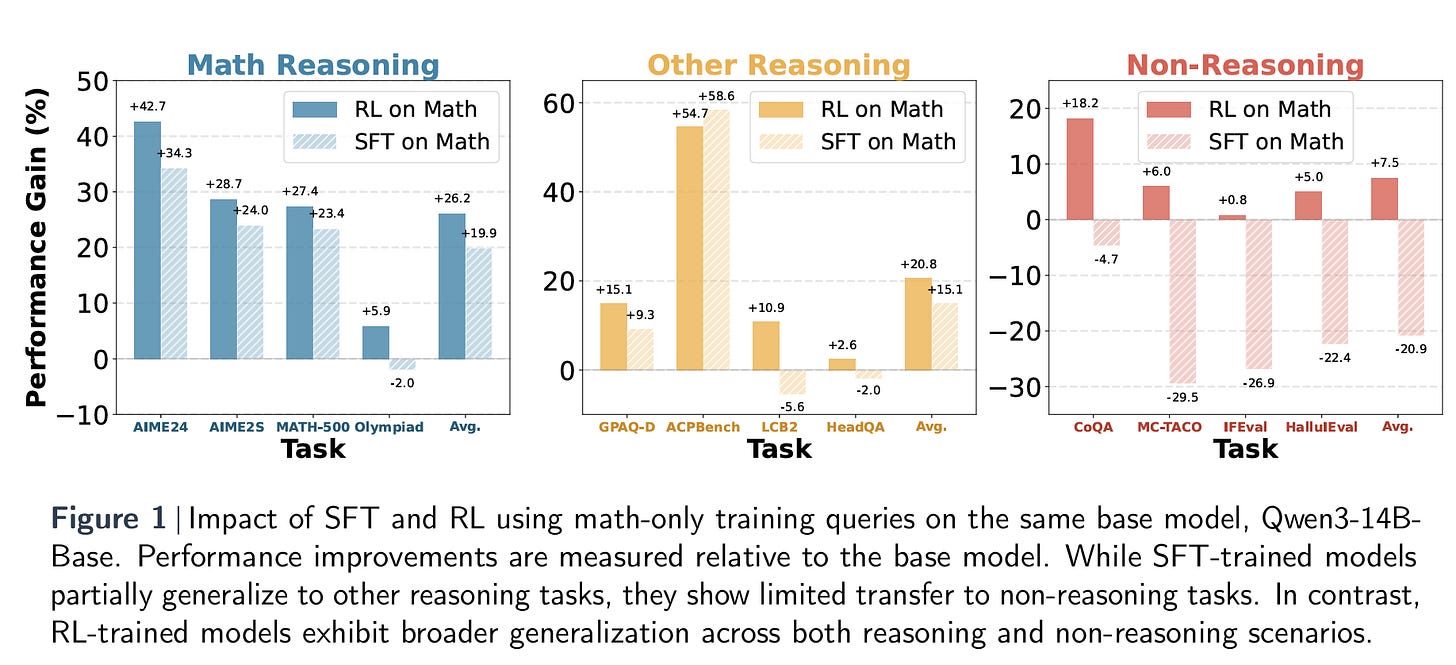
Right upfront, their key conclusion, which is embodied in Figure 1 below is that: RL-tuned models generalize well to non-math domains, despite being trained solely on math queries, while SFT-tuned models do not. This is fascinating, although not completely unexpected. I don’t want to go so far as to call it an ‘emergent’ ability, but it has some of that flavor.

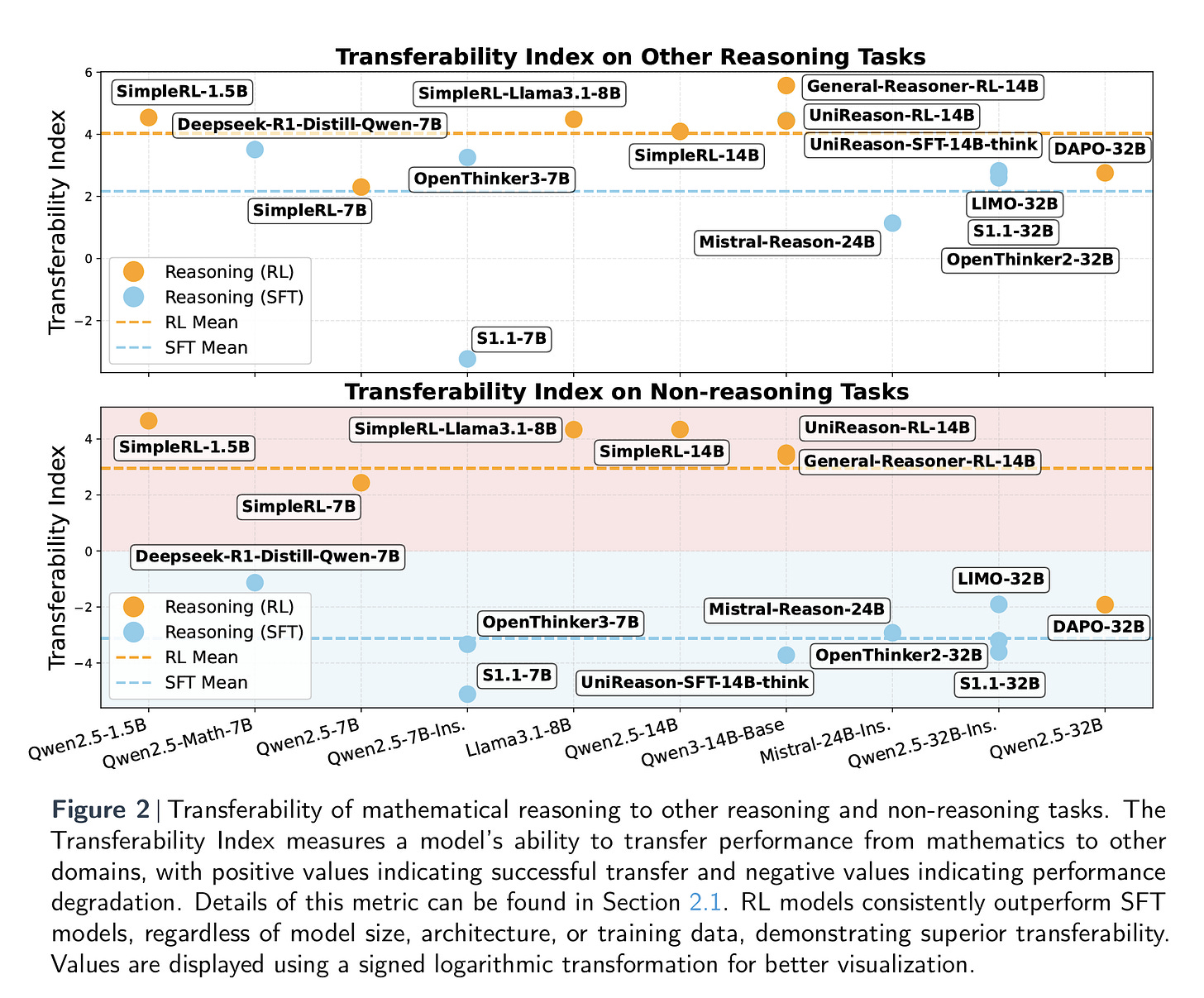
To analyze the issue quantitatively, the authors introduce the Transferability Index, a metric designed to assess how well reasoning models can carry over their capabilities from one domain to another. Interestingly, empirical results show that while some models successfully transfer their enhanced mathematical reasoning to other domains, others do not. This divergence raises a central question: what accounts for the difference?

Although model characteristics such as size, data distribution, and architecture differ significantly, one factor consistently emerges as a key predictor of cross-domain transferability—the fine-tuning paradigm. Models fine-tuned using reinforcement learning tend to generalize more effectively to non-mathematical tasks. In contrast, those trained using supervised fine-tuning often exhibit signs of catastrophic forgetting, performing poorly on a broad spectrum of non-math tasks.

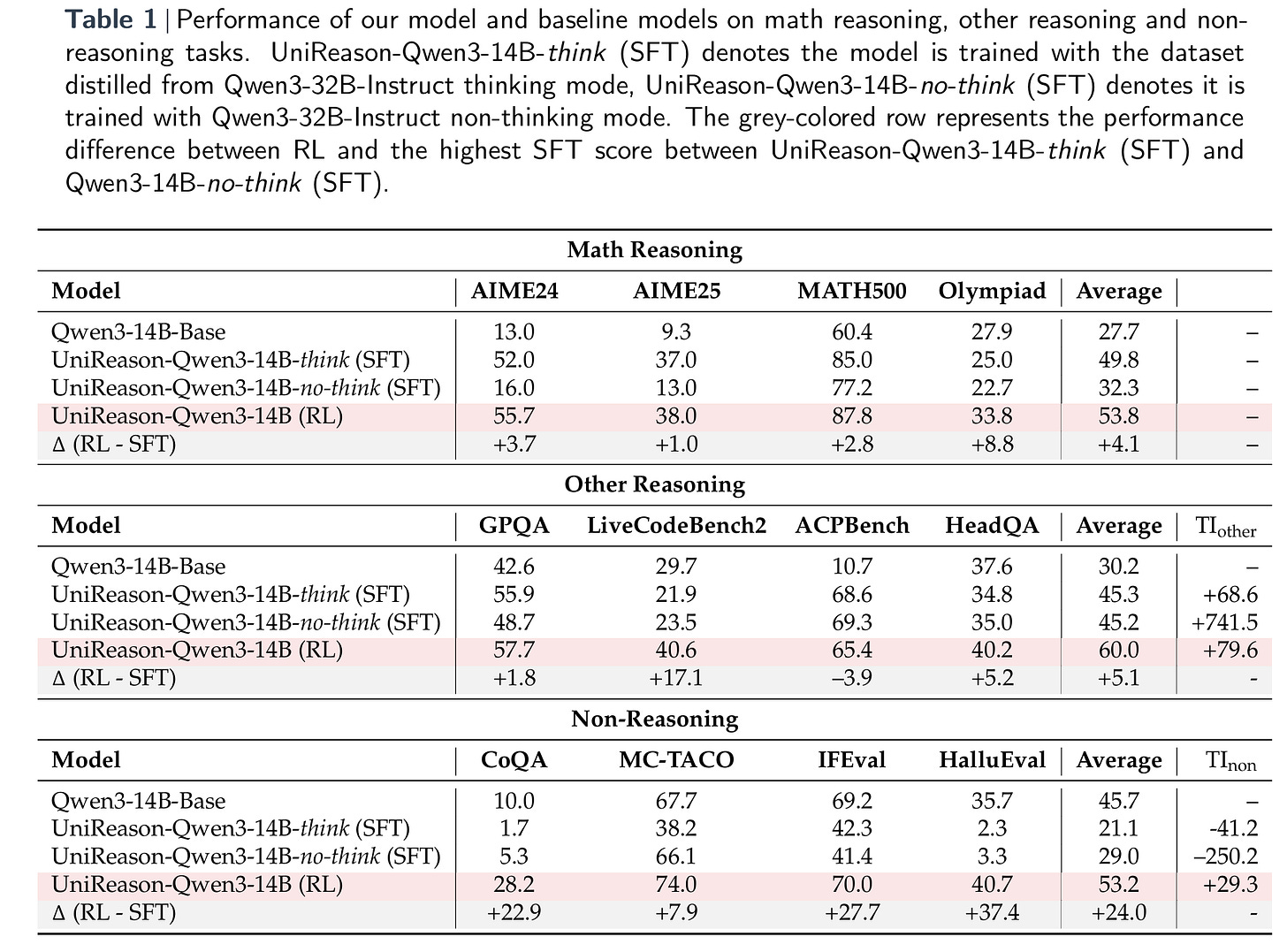
The paper is largely modeled along a lot of experimental results, as opposed to presenting some complex new approach. So let’s jump into some of the other key results. Table 1 below presents the centerpiece of the paper’s controlled study: a direct comparison between RL and SFT on an identical high-quality math dataset using the same base model (Qwen3-14B). The table breaks down performance across three groups of tasks—math reasoning, other reasoning, and non-reasoning—and clearly highlights a consistent trend. While both SFT and RL significantly improve math performance relative to the base model, only the RL-tuned model shows strong gains on non-math tasks. In fact, SFT-tuned models often regress on those tasks, with negative transfer particularly pronounced in the non-reasoning category. This result supports the core thesis of the paper: that the fine-tuning paradigm, more than model size or architecture, is the strongest predictor of whether a model’s math reasoning skills will generalize beyond the domain it was trained on.

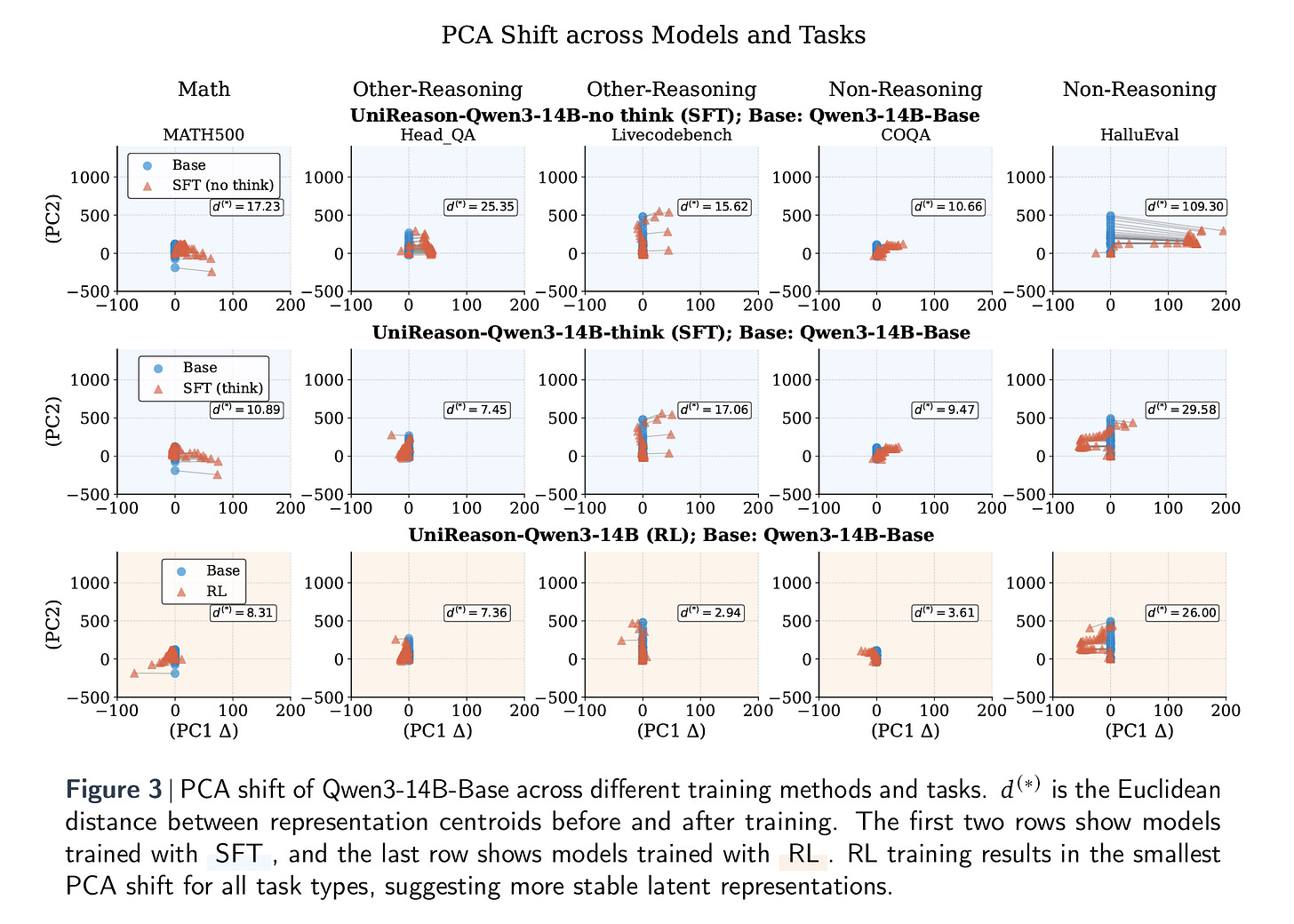
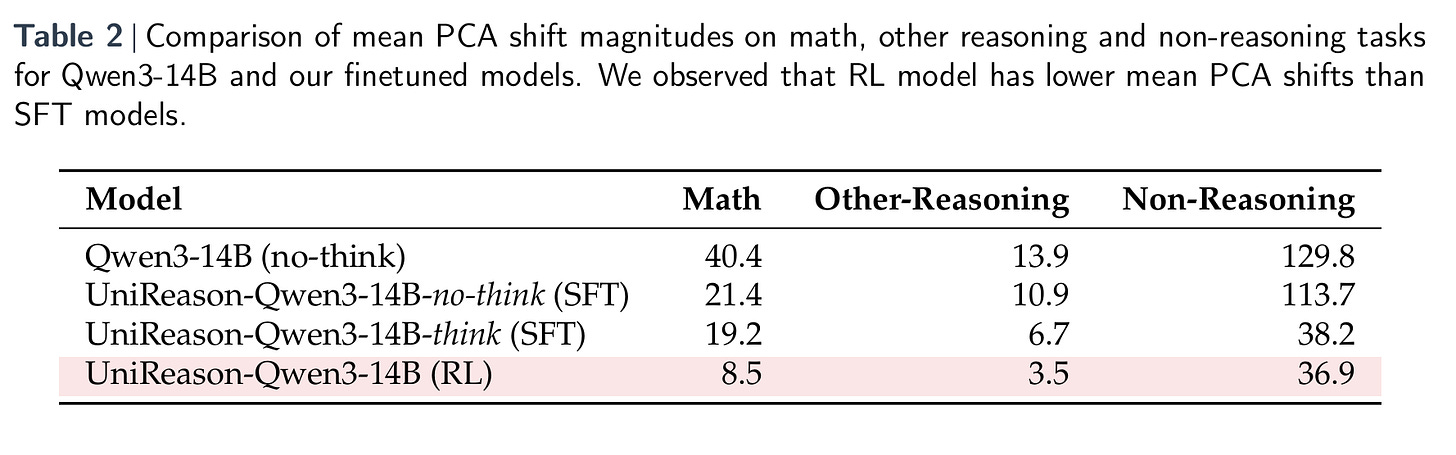
Next, the paper dives beneath surface-level performance metrics to investigate why RL models generalize better than their SFT counterparts. The authors turn to principal component analysis (PCA) to study how the models’ internal latent representations shift during training. The key idea here is that effective transferability should preserve useful internal features rather than overwrite them. Figure 3 below offers a striking visual comparison: across all task types—math, other reasoning, and non-reasoning—RL-tuned models exhibit far smaller PCA shifts than SFT models. This suggests that RL modifies the model’s internal geometry in a more controlled and stable way, maintaining alignment with general-purpose representations rather than distorting them to overfit a narrow task domain.

Table 2 reinforces this finding with quantitative comparisons of the average PCA shift across task categories. The RL model shows consistently lower values, indicating minimal representational drift. In contrast, SFT, especially without “thinking mode”, results in large latent shifts, particularly in non-reasoning tasks. This helps explain why SFT-trained models tend to perform worse outside of their training domain: their internal representations have been skewed or even “collapsed,” reducing their flexibility and robustness. Together, these analyses provide strong evidence that RL doesn’t just yield better performance (it also preserves the foundational structures that support transfer learning).

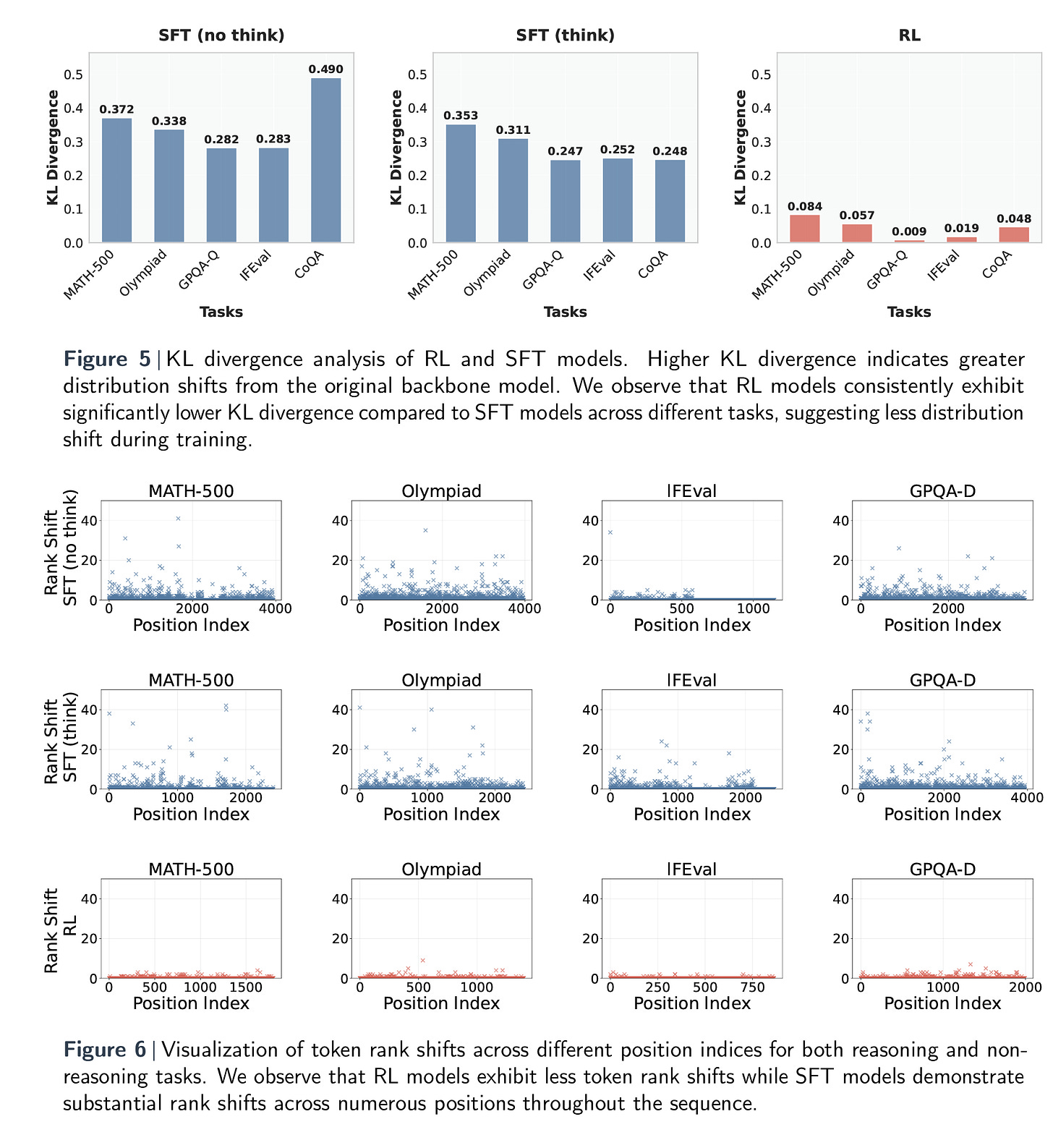
Next, the authors consider how a model’s token distributions and lexical choices are affected by different fine-tuning paradigms. What kinds of words do these models start generating more (or less) often, and are those changes meaningful? To answer this, the authors use two tools: KL-divergence to quantify the overall shift in token probability distributions, and token rank shift to trace how individual word rankings change compared to the base model. The findings are visually captured in Figures 5 and 6 below, which show that SFT models experience far more drastic shifts—both in KL divergence and rank—across tasks.

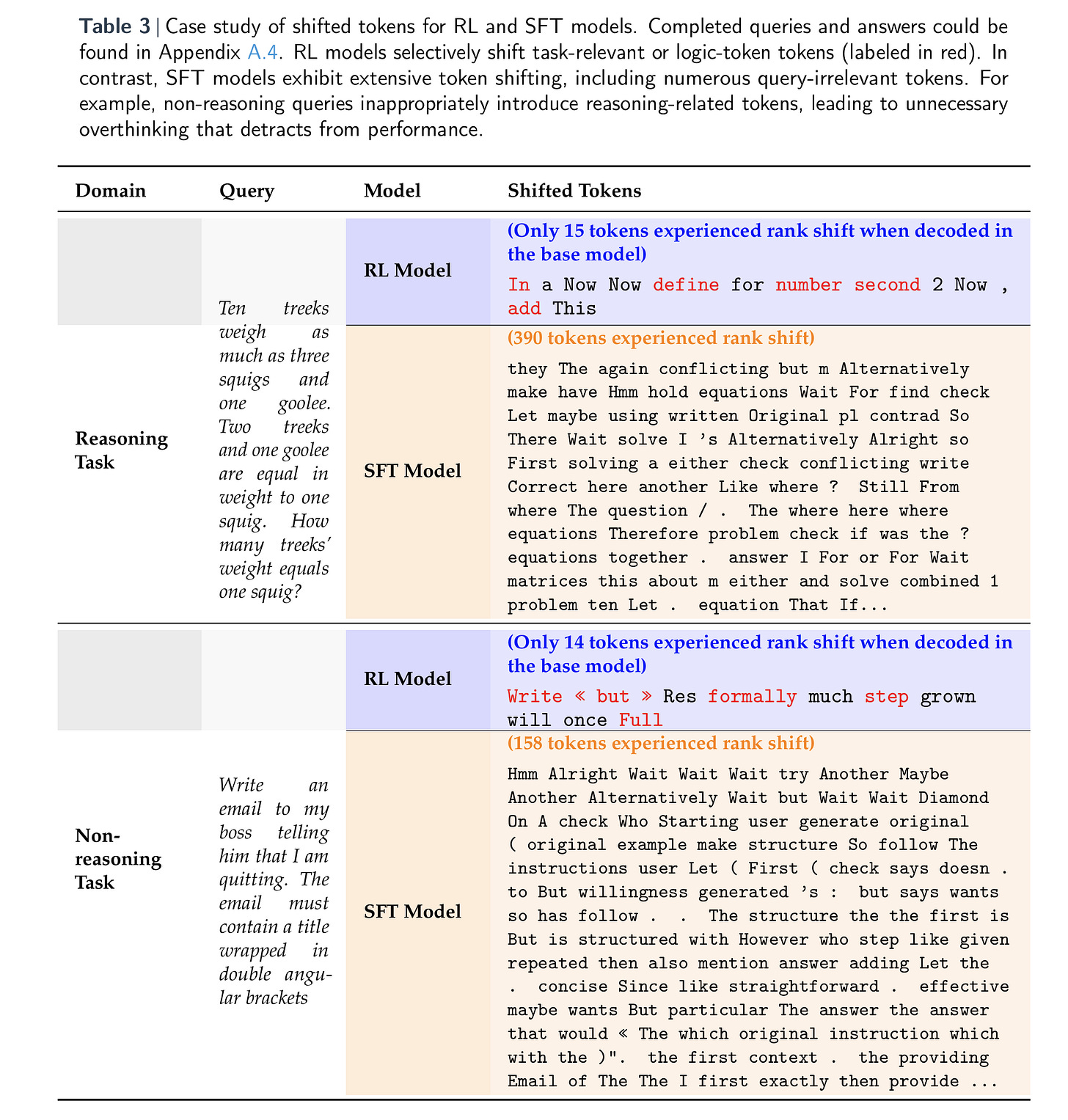
But perhaps the most illuminating evidence appears in Table 3 below, which offers qualitative insight. In math tasks, RL-tuned models make surgical, task-relevant shifts—words like “add,” “define,” and “formally.” SFT models, on the other hand, scatter their attention across a much wider (and noisier) vocabulary, introducing irrelevant tokens even in simple tasks like email writing. This excessive and often unnecessary lexical drift correlates with poorer performance, especially on non-reasoning benchmarks. The implication is clear: RL models preserve not just internal structure, but also disciplined and context-sensitive language generation—qualities essential for real-world generalization.

In closing this musing, the biggest contribution of the article is that how a model is fine-tuned matters just as much—if not more—than what it’s fine-tuned on. The paper’s most striking and unique finding is that RL, even when applied solely to math problems, enables models to generalize effectively across a wide range of domains, including tasks with little or no explicit reasoning. In contrast, SFT, despite producing strong math-specific gains, tends to erode broader capabilities. This suggests that RL doesn't just teach models what to say; it helps shape how they think, preserving latent structure and linguistic discipline that SFT often disrupts.

That said, there are limitations. The study focuses entirely on open-weight models and a particular base (Qwen3-14B), leaving open the question of whether similar trends hold for proprietary models or other architectural families. Also, while RL shows clear benefits, it remains more resource-intensive and harder to scale than SFT. Finally, the evaluation benchmarks, though broader than math, still may not fully capture real-world complexity or user interaction. Nevertheless, this work pushes the conversation forward: instead of simply chasing leaderboard gains, it asks whether those gains are transferable, and offers a blueprint for how to make them so.