Musing 130: Measuring and Analyzing Intelligence via Contextual Uncertainty in Large Language Models using Information-Theoretic Metrics
Interesting paper out of Korea
Today’s paper: Measuring and Analyzing Intelligence via Contextual Uncertainty in Large Language Models using Information-Theoretic Metrics. Jae Wan Shim. 21 July 2025. https://arxiv.org/pdf/2507.21129.
Intelligence remains one of the profound and elusive concepts in science, resisting a single, universally accepted definition. Yet, in recent years, Large Language Models (LLMs) have emerged that exhibit remarkably intelligent-seeming behaviors, achieving human-level performance on a wide array of complex tasks. This success raises a fundamental question: if we struggle to define intelligence, how can we understand the mechanisms that allow these artificial systems to operate so effectively?
Today’s paper sees the advent of LLMs as an opportunity to study this question in depth: “For the first time, systems that exhibit remarkably fluent and complex linguistic behaviors also grant us a transparent window into their predictive reasoning: the complete, high-dimensional probability distribution they generate over their vocabulary for any given context. This granular, quantitative output, derived from the model’s internal logits, offers a novel empirical tool to directly probe the information processing dynamics that underlie these systems’ capabilities.”
The author then proposes a framework built upon the foundational principles of Shannon’s information theory. The author makes an intriguing premise: intelligent information processing operates in a productive tension between two extremes: a purely deterministic response, which lacks creativity, and a purely stochastic response, which corresponds to meaningless noise. A system should be confident when evidence is strong, yet remain open to possibilities when context is ambiguous or creativity is needed. The author terms this fundamental capacity Adaptive Predictive Modulation.
In practice, the author proposes a method whereby one can create a quantitative Cognitive Profile for an LLM. The visualization of this artifact is termed as the Entropy Decay Curve. The shape of this curve—its initial value, decay rate, and asymptotic floor—provides a rich fingerprint of a model’s intrinsic information processing strategy. For more technical readers, the author also clarified that their approach extends beyond the widely used perplexity (PPL) metric. While PPL is related to conditional entropy (h = log_2(PPL)), it is typically reported as a single, averaged score over an entire corpus, obscuring the dynamic effect of context length.
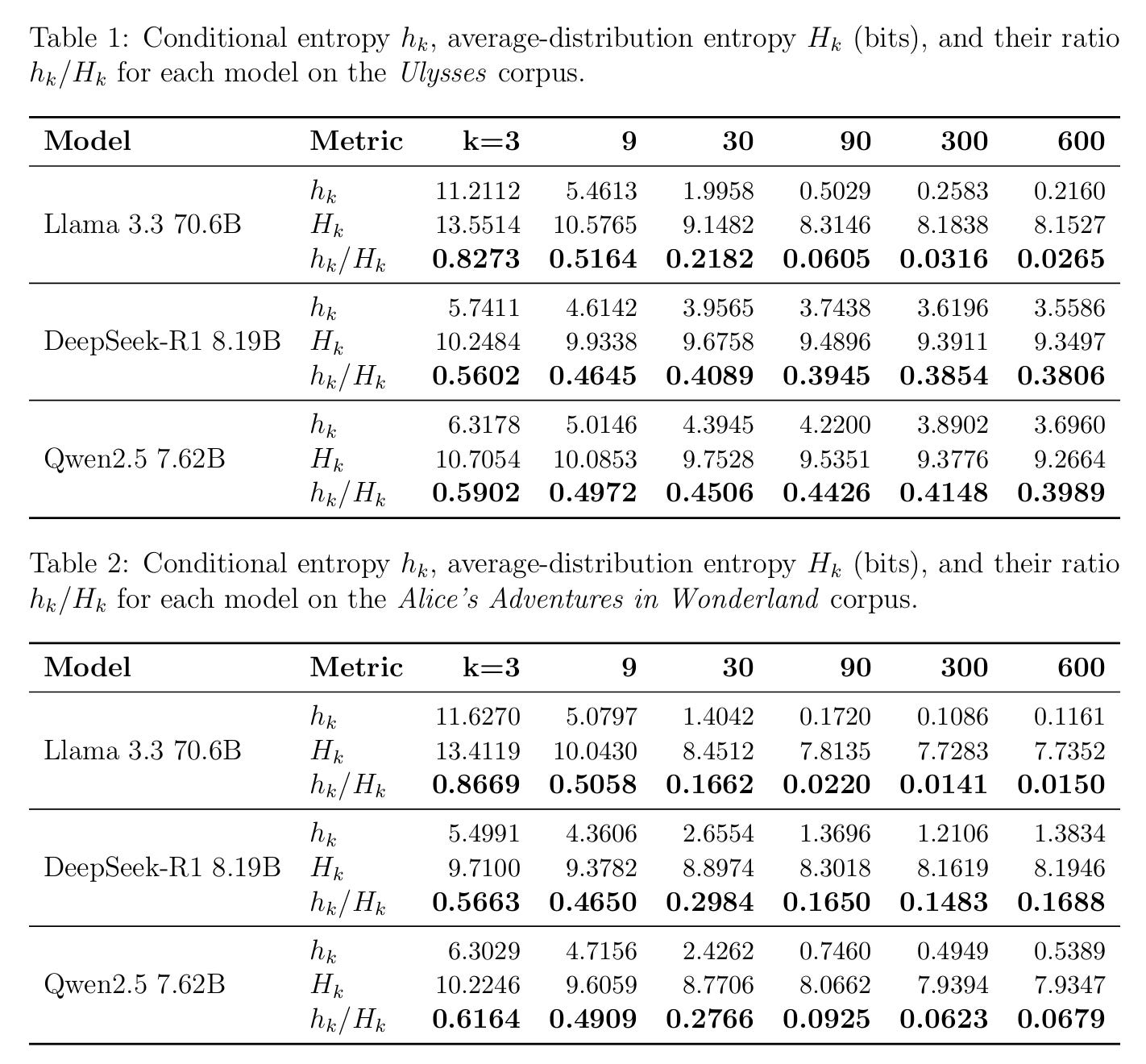
More technically, the author introduces three core information-theoretic metrics—h_k (conditional entropy), H_k (marginal entropy), and u_k (length-conditional uncertainty index=h_k/H_k)—to analyze how LLMs process contextual information and modulate predictive uncertainty. These metrics are designed to go beyond task-specific performance and instead quantify the model's internal dynamics as it processes text. The intuition behind the conditional entropy (h_k) is: how uncertain is the model about its next token prediction, given it has seen exactly k tokens of context? Put differently, given a certain amount of information (k tokens), how much ambiguity remains in the model’s next move? If h_k is high, it suggests the model is unsure, whereas a lower h_k means the model is more certain. Similarly, H_k measures the maximum diversity of predictions the model tends to make across many different contexts of the same length k. Or: “Across a thousand different context windows of this length, how many different next-token predictions does the model find plausible?” Of course, here a thousand is just a sample size to approximate H_k as computing it exactly is intractable. Finally, u_k tells us, “given the size of the space the model considers plausible at context length k, how uncertain is it about what to do in any specific instance?”
Formally, h_k measures the average predictive uncertainty of an LLM when given a context window of length k. For each sampled context x_i from a set of N contexts, the model outputs a probability distribution over possible next tokens. The entropy of this distribution captures the uncertainty for that instance. Averaging over N such windows yields h_k, the expected uncertainty at context length k. A formula and precise calculation is showed in the paper. Similarly, the marginal entropy H_k estimates the diversity of the model's potential outputs for contexts of length k.
Let’s jump to experimental results. Tables 1, 2, and 3 report h_k, H_k, and the derived uncertainty index u_k for all models on Ulysses, Alice’s Adventures in Wonderland, and Kant’s Critique of Judgement, respectively. The primary metric u_k expresses residual prediction uncertainty normalized by the model’s potential output diversity at each context length k. As shown in Table 1 and 2 above, for all models, the conditional entropy h_k monotonically decreases as the context length k increases (from 3 to 600 tokens). This pattern supports a key (albeit obvious) hypothesis: as language models receive more context, their predictive uncertainty decreases. But comparing the two tables (Ulysses vs. Alice), some striking differences emerge: For the same model and context length, entropy values are significantly lower in Table 2 (Alice) than in Table 1 (Ulysses). This demonstrates that the Alice corpus is more predictable and linguistically straightforward for all models, whereas Ulysses—with its complex, stream-of-consciousness style—challenges the models, yielding higher residual uncertainty. This is again cognitively intuitive.
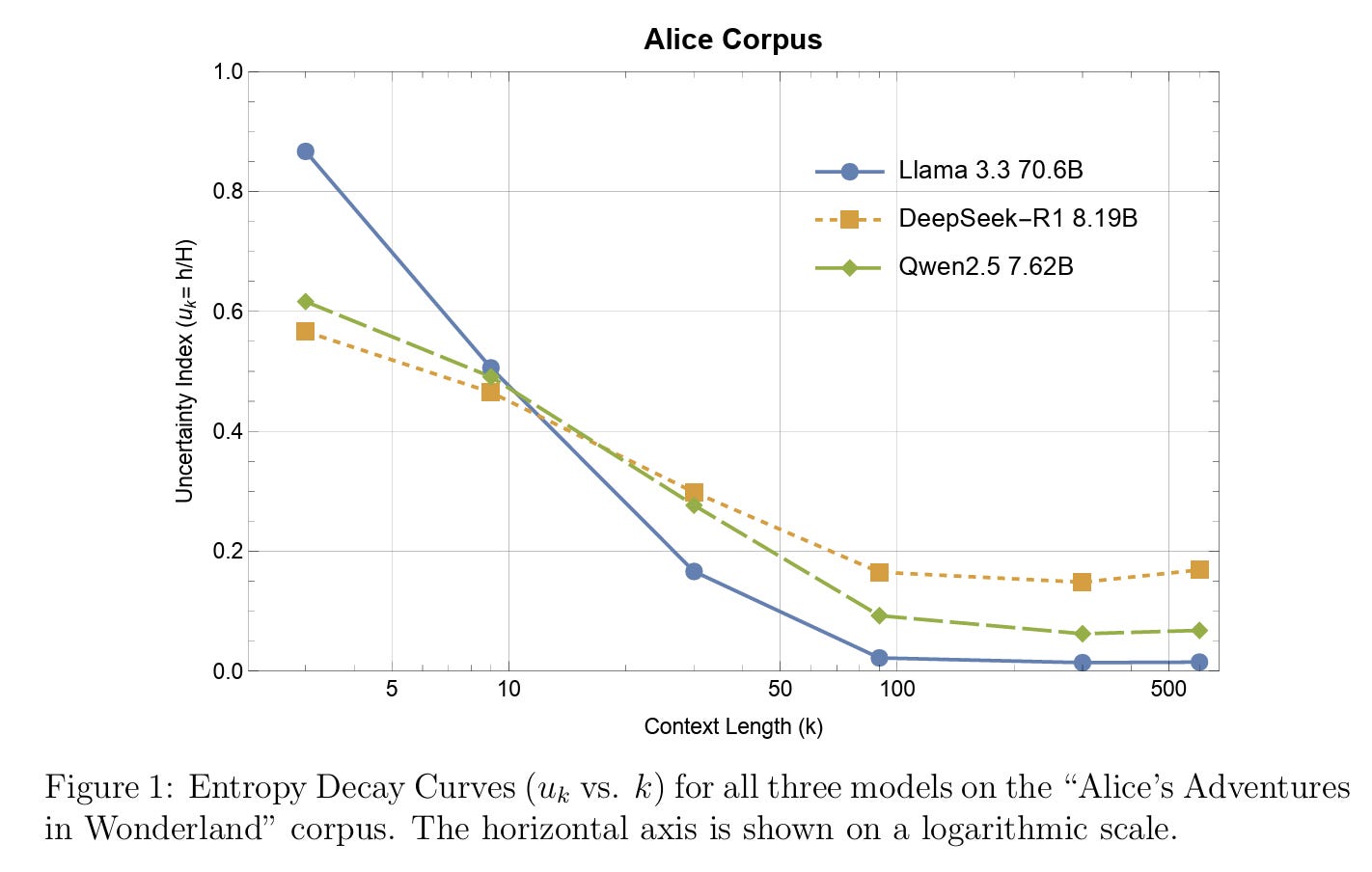
Next, for each corpus and model, the author plotted the Entropy Decay Curve (u_k versus k). Figure 1 above shows the result for Alice, but the paper also has plots for Ulysses and Kant. The figure shows that Llama 3.3’s profile is characterized by extremes. At very short contexts, it consistently shows the highest initial uncertainty suggesting a greater capacity for “divergent thinking.” However, it then demonstrates a dramatic decay, achieving the lowest final uncertainty. This powerful transition from broad exploration to precise inference appears to be a key characteristic of its large scale. Interestingly, in Table 2, Llama 3.3’s final u_k values on Alice are extremely low, indicating extreme certainty, which suggests that the model has memorized portions of the text—especially plausible given Alice is a public-domain classic and likely in its pre-training corpus.
In closing the musing, the author’s empirical analysis shows that the cognitive profiles of LLMs are highly sensitive to (i) model architecture, (ii) parameter scale, and (iii) the intrinsic predictability of the input text. The markedly different decay trajectories traced by Llama 3.3, DeepSeek-R1, and Qwen 2.5 reveal distinct strategies for leveraging contextual information. The author also demonstrates the utility of this method as a powerful diagnostic tool for identifying anomalous predictive behavior. The phenomenon of “entropy collapse,” observed with the Llama 3.3 model on the Alice corpus, serves as a key finding. While not definitive proof, such an anomaly provides strong, quantitative evidence that is highly consistent with the hypothesis of memorization due to pre-training data contamination. This offers a principled framework for a more fundamental understanding of the reasoning patterns in an AI.
My own thoughts are that the paper contains lots of really interesting and tantalizing ideas. The empirical results are preliminary, leaving the door open for a stronger paper that uses more models, more data, and explores some of the ideas that the author presents in greater detail. If any researchers are reading this, and looking for a good idea to pounce on for that next NeurIPS paper, this paper may have something for you.