Musing 31: Geometry Problem Solver with Natural Language Description

A recently accepted NAACL 2024 findings paper from the University of Strathclyde

Today’s paper: GOLD: Geometry Problem Solver with Natural Language Description. Zhang and Moshfeghi. May 1, 2024. https://arxiv.org/pdf/2405.00494

Automated solving of geometry math problems has recently attracted significant interest in the artificial intelligence community. These problems differ from math word problems as they include geometry diagrams, requiring advanced reasoning to understand multi-modal information. An example of a geometry math problem typically showcases these challenges.

Despite growing interest, research in this area is still nascent. Current methods primarily use neural networks to process diagrams and problem text, either separately or together, creating generalized models. Yet, these models often fail to accurately depict the complex relationships within geometry diagrams. Moreover, their vector-based representation of geometric relationships is hard for humans to interpret, making it difficult to pinpoint whether issues arise from extracting relationships or solving the problem itself.

Alternatively, some researchers have translated geometry diagrams into formal languages to improve precision and interpretability. Nonetheless, these techniques do not differentiate between relationships among geometric shapes and those between symbols and shapes, complicating the problem-solving process. Additionally, these methods require specialized solvers that accept formal languages, which are not compatible with the more common large language models.

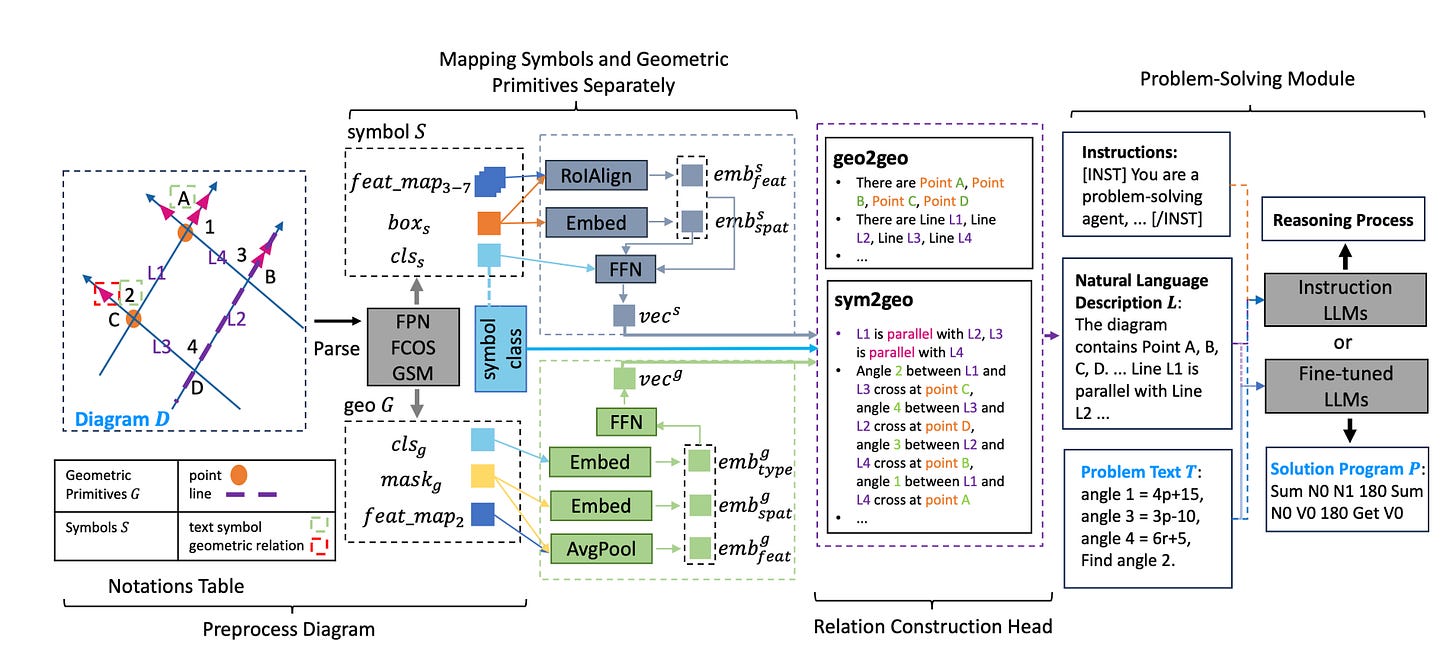
In today’s paper, the authors propose the GOLD framework. The GOLD model transforms geometry diagrams into natural language descriptions, facilitating the creation of solution programs for the problems. Specifically, the GOLD model features a relation-construction head that identifies two kinds of geometric relationships: sym2geo (relations between symbols and geometric primitives) and geo2geo (relations among geometric primitives). This function is carried out by two specialized heads that model symbols and geometric primitives as separate vectors within the diagrams. These geometric relationships are then translated into natural language descriptions, enhancing the model's interpretability and linking the geometry diagrams with the associated problem texts.

Moreover, since these natural language descriptions align with the input standards of large language models (LLMs), the GOLD model can employ advanced LLMs as its problem-solving module, effectively generating solution programs to tackle geometry math problems. An architecture of GOLD is shown below.

There are a lot of interesting things going on in the model, but as with so many papers of this nature, the proof is in the pudding. So let’s get straight to the experiments. They use three datasets: UniGeo, PGPS9K, and Geometry3K. The UniGeo dataset includes 14,541 problems, split into 4,998 calculation problems and 9,543 proving problems. These are divided into training, validation, and testing subsets in a ratio of 7.0:1.5:1.5. The Geometry3K dataset contains 3,002 problems, distributed across training, validation, and testing subsets in a 7.0:1.0:2.0 ratio. Since the PGPS9K dataset incorporates part of the Geometry3K dataset, an exclusive set of 6,131 problems was maintained, with 1,000 of these designated as a test subset. Due to the lack of a validation subset in PGPS9K, the training set was split to create a train-validation split in a 9.0:1.0 ratio.

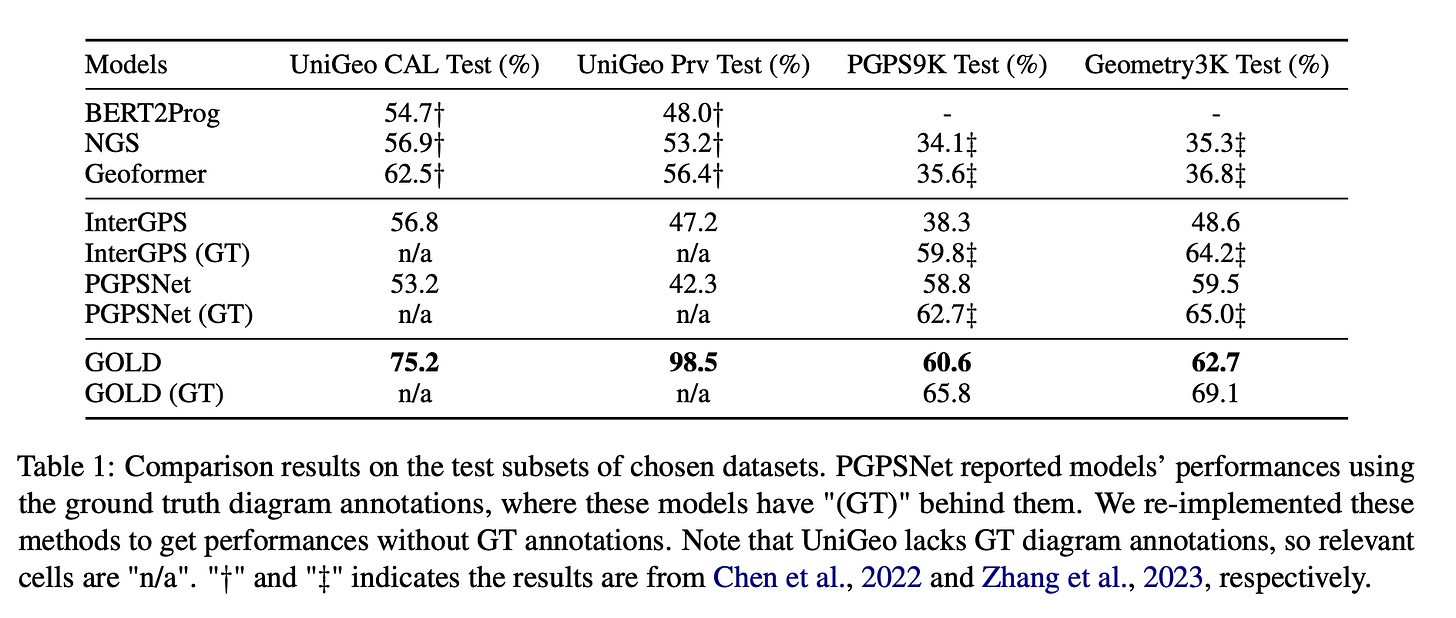
Performance is evaluated against state-of-the-art (SOTA) methods in solving geometry math problems, including PGSPNet, InterGPS, Geoformer, NGS, and Bert2Prog. The table below demonstrates the competitiveness of their method against these baselines on the datasets.

In closing, I want to note that the method does have some limitations. It does not yet reach the level of human performance in solving geometry math problems (but that might just be a question of when, not if). This gap is possibly due to the limitations in fully extracting geometric relations from diagrams. While GOLD accurately identifies symbols, geometric primitives, and geo2geo relations, the extraction of sym2geo relations still requires enhancement. Moreover, this study evaluated three popular large language models (LLMs): T5-bases, Llama2-13b-chat, and CodeLlama-13b. Obviously, it would be beneficial to assess more LLMs.

However, the purpose of the paper is very interesting and shows how many interesting multi-modal applications are now starting to open up because of ongoing progress in LLMs.