Musing 38: The Platonic Representation Hypothesis

A very interesting paper on the nature of representations being learned by neural networks.

Today’s paper: The Platonic Representation Hypothesis. Huh et al. 13 May 2024. https://arxiv.org/pdf/2405.07987

Some research papers are interesting because they improve over the state of the art with a novel idea, and others because they present a new problem. Today’s paper is interesting because it presents a thought-provoking idea, not completely surprising, but valuable to put into words and argue scientifically.

The title of the paper suggests what I’m talking about and is called the platonic representation hypothesis. The figure from the paper expresses it best:

The authors first claim that “AI systems are becoming increasingly homogeneous in both their architectures and their capabilities.” They then zoom in on one aspect of this trend: representational convergence. They argue that there is a growing similarity in how datapoints are represented in different neural network models. This similarity spans across different model architectures, training objectives, and even data modalities. One could argue by extension that, given the exceedingly impressive performance of these models, that this converged representation is the computationally closest version of reality that we’ve got (in theory, not the only possible one).

The authors ask the questions: What has led to this convergence? Will it continue? And ultimately, where does it end?

One thing I immediately like about the paper is that the authors avoid the danger of going too much into philosophy, and stick to the technicals. On the second page, they provide some concrete, important definitions about the concepts noted above to set the stage. Because it’s cumbersome to write equations properly in substack, I’ll paste it in as a figure here:

Closely related to the authors’ hypothesis is the “Anna Karenina scenario” described by Bansal et al. (2021), referring to the possibility that all well-performing neural nets represent the world in the same way. The platonic representation hypothesis refers to a ‘next step’ situation where the authors argue that “we are in an Anna Karenina scenario and the happy representation that is converged upon is one that reflects a statistical model of the underlying reality.”

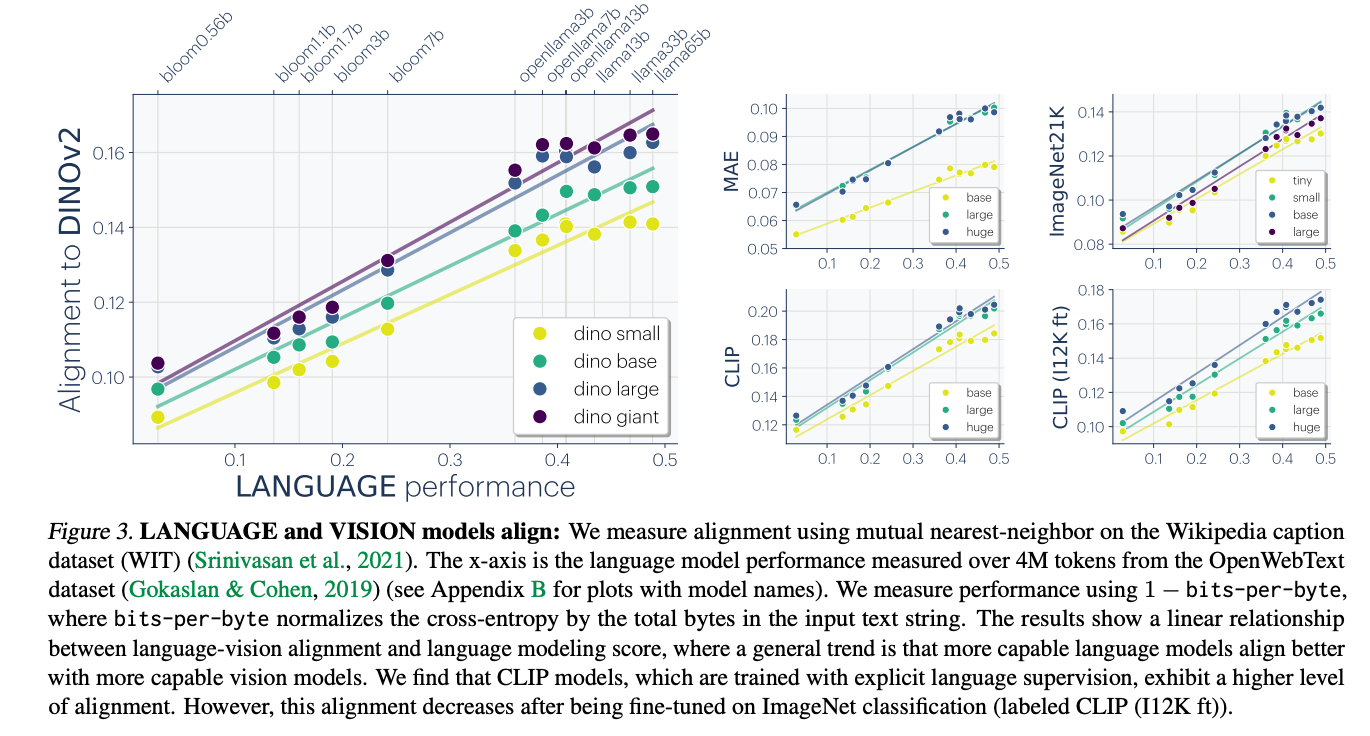
Without going into all the details of the authors’ survey on the evidence for convergence, it’s good to see just what some of this evidence says. A striking claim is that, especially since the advent of multimodal GenAI, representations are converging across modalities:

The authors also present some other interesting hypotheses, based on their survey of their evidence, that are worth reproducing here:

The multitask scaling hypothesis: There are fewer representations that are competent for N tasks than there are for M < N tasks. As we train more general models that solve more tasks at once, we should expect fewer possible solutions.

The capacity hypothesis: Bigger models are more likely to converge to a shared representation than smaller models.

The simplicity bias hypothesis: Deep networks are biased toward finding simple fits to the data, and the bigger the model, the stronger the bias. Therefore, as models get bigger, we should expect convergence to a smaller solution space.

Personally, I have some reservations against both the simplicity bias and capacity hypotheses. For one, the capacity hypothesis depends clearly on the size of the data on which the representations are being learned. Without specifying the data, it is easy to come up with arguments that both support and refute the hypothesis under the right circumstances. Moving on to the simplicity bias hypothesis, I wonder what simplicity really means here and how we characterize the simplicity of a solution space. Intuitively, my understanding is that a model with fewer parameters or assumptions would ordinarily be considered simpler (hence, we consider a linear regression simpler than a cubic polynomial). But I’m not sure that simplicity in model space transitions naturally to simplicity in ‘solution’ space. At the very least, there are some interesting conceptual challenges to grapple with there.

To their credit, the authors do go into counterexamples and limitations of some of their hypotheses. They admit, for example, that not all representations are converging and in domains like robotics, there is not yet a “standardized approach to representing world states in the same way as there is for representing images and text.” Also, right at the beginning of the paper, the authors make it clear they are talking about vector embedding representations, which form the basis for all deep learning architectures. In AI, we’ve always had a healthy debate, even tension, between such real-valued ‘continuous’ representations and symbolic representations. Cognitively, symbols play an important role in our own thinking and reasoning, and one could argue that without a symbolic component, DNNs are only as good as the huge amounts of data they are trained on. In practice, this may not be a problem, but it leaves open the door to other more efficient representations than the ones the authors are primarily centering on.

In the end, the paper is a fascinating take on the nature of representation itself. I highly recommend it for anyone who wants to learn more about learning, and why neural networks ultimately do so well. There is a lot more to representation than meets the eye, and the authors are giving us a window into all of that with this paper.