Musing 55: Q*: Improving Multi-step Reasoning for LLMs with Deliberative Planning
A paper out of Skywork AI and Nanyang Technological University
Today’s paper: Q*: Improving Multi-step Reasoning for LLMs with Deliberative Planning. Wang et al. 20 June 2024. https://arxiv.org/pdf/2406.14283
While it is almost cliched now to say that LLMs have achieved really impressive feats, solving complex reasoning problems requires more in-depth, deliberative and logical thinking steps, i.e., what Daniel Kahneman called the “System 2" mode of thinking. Whether LLMs are really able to do such complex reasoning by themselves is not a slam-dunk case; on a pragmatic front, we need to prompt or otherwise include the LLM in a larger architecture (with other components) to achieve good performance on difficult reasoning tasks.
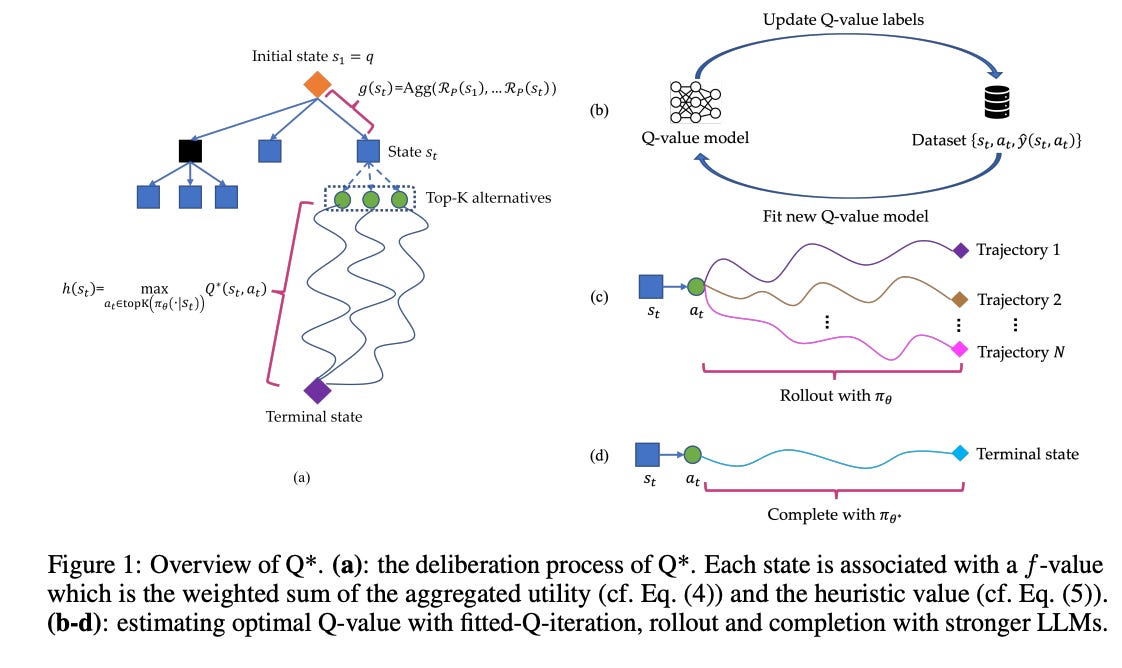
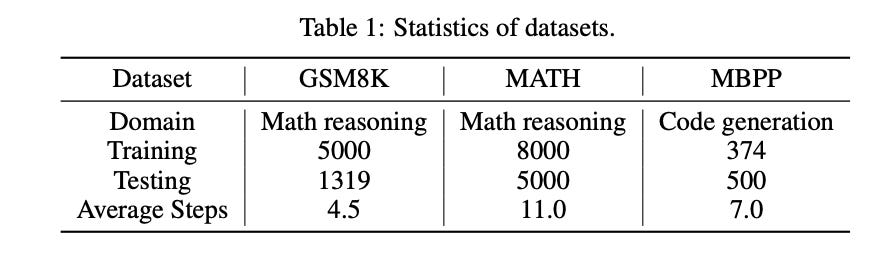
Today’s paper proposes Q*, a “general, versatile and agile framework for improving the multi-step reasoning capability of LLMs with deliberative planning.” Their method does not rely on domain knowledge to design the heuristic function, but rather, they formalize the multi-step reasoning of LLMs as a Markov Decision Process (MDP) where the state is the input prompt and the reasoning steps generated so far, the action is the next step of reasoning and and the reward measures how well the task is solved. They then present several general approaches to estimate the optimal Q-value of state-action pairs, i.e., offline reinforcement learning, best sequence from rollout and completion with stronger LLMs. Their methods only need the ground truth of training problems and can be easily applied to various reasoning tasks without modification:
Finally, they cast solving multi-step reasoning tasks as a heuristic search problem, where the objective is to find the most proper reasoning trace with maximum utility (see above). Built upon A* search, their deliberation framework, Q*, leverages plug-and-play Q-value models as heuristic function and guides LLMs to select the most promising next reasoning step in best-first fashion.
The paper itself goes into some math behind the steps above, and interested readers can aim to study it in depth. But as with so many other musings, the proof is really in the experiments, so let’s dive into those. The authors use several benchmark datasets in complex problem solving:
GSM8K is a dataset of grade school math problems, where the solution is given in a one-line-per-step format with an exact numerical answer in the last line; MATH is a dataset consisting of math problems of high school math competitions, where the solutions are given in a format that mixes latex code and natural language; MBPP is an entry-level Python programming dataset, where the questions are coding challenges along with a test case that defines the function format. The solutions are Python code that is excepted to pass the pre-collected test cases of each question.
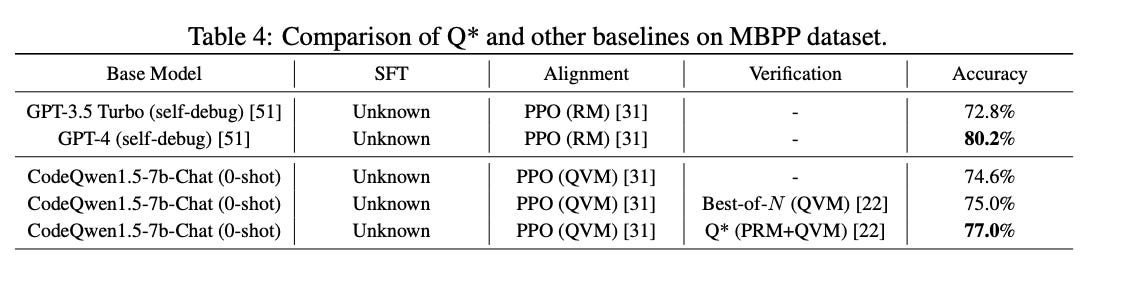
For the comparison on the GSM8K dataset, Llama-2-7b was selected as the base model, achieving 65.2% accuracy after finetuning on MetaMath. This finetuned model, referred to as policy πθ, was used to perform rollout and collect Q-value labels for training a Q-value model (QVM). For aggregated utility, a process reward model (PRM) was trained on PRM800K to provide intermediate signals for each reasoning step. With both PRM and QVM available, traditional methods either treat one as a verifier to select the Best-of-N trajectory or use them for PPO training of RLHF. Results in Table 2 below indicated that verification using PRM/QVM performs significantly better than alignment. Additionally, in the comparison of planning-based methods, the Q* method with constant aggregated utility outperforms the Best-of-N method when using the same QVM. The Q* method, combining PRM and QVM, achieved the best performance among methods based on the Llama-2-7b model, surpassing the performance of the closed-source ChatGPT-turbo.
Regarding the MATH dataset, due to the weak performance of Llama-2-7b fine-tuned on MetaMath, two stronger base models were chosen to evaluate the effectiveness of the Q* method: Llama-2-7b fine-tuned on Synthetic Data, achieving 41.9% accuracy (see Table 3 below), and DeepSeek-Math7b, achieving 50.8% accuracy. Results indicated that the Q* method leads to further performance improvements compared to the Best-of-N method. The performance of Q* based on DeepSeek-Math-7b surpassed several closed-source models on the MATH dataset leaderboard.
For the comparison on the MBPP dataset (Table 4 below), CodeQwen1.5-7b-Chat, the most powerful open-source LLM for code generation, was chosen as the base model to evaluate the effectiveness of Q*. Following a similar procedure to math reasoning, a QVM was trained for Q-value estimation, and a heuristic function was manually constructed. Results showed that the Q* method outperforms the Best-of-N method in code generation, achieving 77.0% on the MBPP dataset, a promising performance on the leaderboard.
In closing, solving challenging multi-step reasoning problems requires LLMs to perform in-depth deliberation beyond auto-regressive token generation. The paper presents one such approach, called Q*, which is claimed to have some beneficial properties. For instance, the authors claim that Q* is agile because it considers only a single step each time rather than complete rollouts (e.g., simulation in MCTS). Whether it becomes a standard baseline or is quickly superseded by other methods remains to be seen.