Musing 76: Causal Language Modeling Can Elicit Search and Reasoning Capabilities on Logic Puzzles
Paper on causal LM out of Google Research and (my alma mater) UT Austin
Today’s paper: Causal Language Modeling Can Elicit Search and Reasoning Capabilities on Logic Puzzles. Shah et al. 16 Sept. 2024. https://arxiv.org/pdf/2409.10502
Over the past few years, employing causal language modeling with transformer architectures has significantly improved the capabilities of Large Language Models (LLMs). However, there is ongoing debate about how much fundamental search and reasoning skills have developed within these models. For example, while LLMs demonstrate impressive performance on benchmarks that demand advanced reasoning and planning skills, like MATH, HumanEval, and others, some research indicates that these abilities can be highly fragile or, in some cases, the model might merely be executing 'approximate retrieval.'
In today’s paper, the authors study whether causal language modeling can learn to perform complex tasks such as solving Sudoku puzzles and ‘Zebra’ puzzles. While the former is more familiar to readers, the latter a more verbal style of a puzzle (see Figure 1 below) where we need to fill in values in a grid again but this time the type of possible constraints is much richer. These are also known as Einstein riddles.
Obviously, there is some precedence for such studies, especially since the emergence of ChatGPT. Prior research has studied how causal language modeling with transformers performs on synthetic tasks such as learning how to make valid moves in Othello, learning context-free grammars, learning deterministic finite automata and learning specific algorithmic tasks. Compared to these, however, Sudoku puzzles present a more challenging task. For the computer scientist, it may not be surprising to know that solving Sudoku on an n X n grid is NP-Complete (for the non-computer scientist, this simply means the problem is ‘very hard’). Same is the case for Zebra puzzles.
Of course, if the puzzles are just too hard and the LLMs fail completely, that would make for a trivial reading. For this reason, the authors consider a class of logic puzzles which can be solved in polynomial time. This class still remains non-trivial to learn. For an idea of how challenging these can be, the authors performed a small experiment on how well some frontier LLM’s of today can solve Sudoku puzzles. They prompted them in a 4-shot manner with 4 Sudoku puzzles (they serialize a puzzle by converting it into a sequence of (row, column, value) triplets) and their corresponding solutions given before asking for the solution for a 5th test Sudoku puzzle. They evaluated 3000 examples on Gemini-1.5 Pro and GPT-4o. They observed that neither models are able to solve any of the puzzles fully correctly:
Let’s move on to the setup of the study. The authors frame each Sudoku and Zebra puzzle as a sequence-to-sequence problem. For Sudoku, the model is given the sequence of filled cell positions and their values, and it must output the sequence of unfilled cell positions and their values. In the Zebra puzzle, all clues and potential values for characteristics are provided sequentially, requiring the model to predict the values in the grid. To focus on the model's reasoning, they use a symbolic version of Zebra puzzles, referring to each person as an entity indexed by a number, with attributes like favorite color or car also represented numerically.
The order of solutions presented to the model during training significantly impacts performance. The authors use a dataset of Sudoku puzzles varying in difficulty and a Sudoku solver with 7 human-like strategies to solve them, resulting in 1.9 million examples. For Zebra puzzles, they generate around 320,000 examples of varying sizes, ensuring all are solvable efficiently. Their solver adds clues iteratively until it can solve the puzzle, running in cubic time relative to the number of clues. This approach ensures that both Sudoku and Zebra puzzles are solvable in polynomial time, with a high probability that the train and test sets do not overlap.
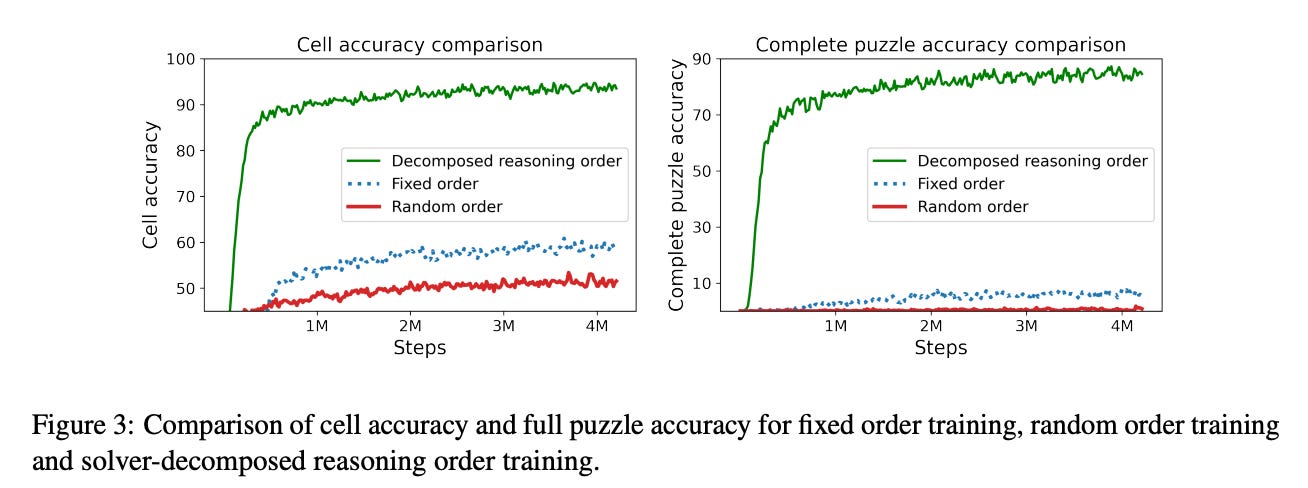
Moving on to results (always the central contribution in such studies) the authors mainly focus on the Sudoku puzzles to explain their results and only include a brief discussion on the Zebra puzzles. The first experiment studies whether a transformer is capable of solving the Sudoku puzzle in a fixed cell order (from top-left to bottom-right). This would amount to the model knowing what values to fill in each unfilled cell in a single forward pass. They observe that although the model learns to predict the values for some cells in a puzzle (average cell accuracy 58.64% across all unfilled cells), in general, this leads to poor accuracy of solving the complete puzzle (7.2%).
Next, the authors try chain-of-thought (CoT) prompting. Solving the sudoku puzzle can be decomposed into two sub-tasks: 1) Search across the board to find the cells that are easy to fill and 2) After finding the easy-to-fill cell, apply the correct strategy on the cell to obtain a correct value in it. The authors use this intuition to construct a CoT strategy. The figure below shows that using the decomposed reasoning order achieves the cell accuracy 94.23 % and complete puzzle accuracy 87.18% accuracy. Training the model on the decomposed reasoning order improves cell accuracy by around 36% over the fixed-order training and by around 43% over the random-order training. The most noticeable improvement comes in complete puzzle accuracy where decomposed reasoning order training achieves 87.18 % accuracy whereas the fixed-order training achieves around 8 % accuracy and the random-order training achieves around 1 %.
Other strategies are tried next, including on Zebra, but a particularly important one that I want to cover as part of this musing tries to simulate human reasoning more accurately in solving the puzzles. As noted earlier, a model trained with puzzles given in solver-decomposed reasoning order performs very well. The authors ask how the model is learning such a task that requires planning and reasoning. One viable theory specifically for the sudoku solver (and to an extent humans) is that it keeps track of possible values that a cell can take for the given puzzle. Does the model also keep track of possible values of a cell? Can they be extracted from the model?
The authors answer both of these questions (perhaps surprisingly) positively by showing that for a given puzzle, the candidate set of the solver can be extracted from the logits of the model. The candidate set of an empty cell keeps track of possible values that the cell can take given a state of the puzzle. Note that given some state of the puzzle, the candidate set at an empty cell (r, c) can be different from {1, 2, . . . , 9} − {set of filled values in row r, column c and box b(r, c)} as some of the strategy removes a value which does not occur in the same row, column or box.
Without going into all the gory details, the results of candidate set equivalence accuracy (as they call it) are given in the table below:
For all positions the average overlap between the solver’s and the model’s candidate set is above 93 %. This overlap improves to around 96.5 % when the prefix has information about 60 cells and to around 98.5 % when the prefix contains information about 70 cells. This is impressive because the candidate set equivalence result is not only for cells that are easy to decode but for all empty cells. Moreover, during the training of the model, no direct information about the candidate set is provided and the model is only trained to predict the correct value for a cell and therefore is not directly incentivized to predict the correct candidate set for all the empty cells with such a high accuracy.
Here are the key takeaways:
Causal language modeling with the transformer architecture is capable of learning to perform search and reasoning in highly non-trivial domains like Sudoku and Zebra puzzles.
The authors present evidence that the right form of training data which decomposes the problem into smaller constituents is crucial. However this data is not required to be too descriptive. In particular, it need not contain search traces similar to those provided in prior work.
The authors perform a probing analysis to show that human-like abstract reasoning concepts such as candidate set of values emerge implicitly within the model’s activations.
To re-emphasize what I think is the most important takeaway, the authors conclude that “given the right level of detail and breakdown of reasoning steps in the training data, a pre-trained model might already present as a strong reasoning engine (without the need for post-training techniques such as fine-tuning, prompt engineering, self-consistency, tree-of-thoughts etc). These techniques might help significantly boost the baseline performance of a model or potentially make up for deficiencies in the pre-training data however.”
I’ll close by noting that the study does not have important limitations. The authors studied a synthetic setting on a toy task and real-world reasoning and planning tasks can be much more abstract and challenging. More specifically, Sudoku is a task which doesn’t require the same degree of long-term planning as some harder benchmarks. That is, any cell that can be made progress on is progress unlike constraint problems where one might need to backtrack. Moreover, the authors focused on a reasoning setting where creative thinking was not required. That is, the model did not need to invent new strategies to solve any test time puzzle. It is an interesting future direction to study to what extent causal language modeling can yield novel reasoning strategies.