Musing 81: DOTS: Learning to Reason Dynamically in LLMs via Optimal Reasoning Trajectories Search

Fascinating paper out of George Mason University and Tencent AI

Today’s paper: DOTS: Learning to Reason Dynamically in LLMs via Optimal Reasoning Trajectories Search. Yue et al. 4 Oct. 2024. https://arxiv.org/pdf/2410.03864

Large Language Models (LLMs) have shown impressive ability in solving complex reasoning tasks, including mathematical, symbolic, and commonsense reasoning. The main methods for improving reasoning capabilities in LLMs are instruction tuning and prompt engineering. Instruction tuning involves collecting question-answer pairs related to reasoning tasks and using supervised fine-tuning to improve the LLM's reasoning performance, with recent work focusing on expanding the scale and quality of the fine-tuning data. In contrast, prompt engineering aims to design more effective prompts to elicit reasoning from an LLM without changing its parameters. The Chain-of-Thought (CoT) approach prompts the LLM to answer reasoning questions step by step in natural language, while program-aided methods prompt the LLM to write executable code, which is then run through an interpreter to derive the final result.

Both methods unfortunately suffer from some limitations and that’s where today’s paper comes in: they are unable to dynamically select the best reasoning strategies. In instruction-tuning-based methods, fine-tuned LLMs are restricted to the reasoning format used in the training data and lack the flexibility to adopt alternative strategies. Similarly, prompt engineering relies on predefined prompting strategies that are applied uniformly to every question, despite the fact that different types of questions may require different reasoning strategies. The effectiveness of a prompting approach also depends on the inherent capabilities of the LLM, such as whether it was pre-trained on code data, which may make it more suitable for programming-aided reasoning. As a result, a single prompt may not be equally effective for all questions or for every LLM.

The authors propose DOTS (reasoning Dynamically via Optimal reasoning Trajectories Search), which is tailored to the specific characteristics of each question and the inherent capability of the task-solving LLM. Prior studies have validated the effectiveness of various reasoning strategies (Table 1 below). The authors build on top of them and categorize the existing strategies as reasoning actions across three layers:

Analysis Layer Actions in this layer enable the LLM to analyze the input query before attempting to solve it, including (1) Query rewriting: reformulating the query to enhance comprehension, and (2) Query decomposition: breaking down the initial question into multiple, more manageable sub-questions.

Solution Layer Actions in this layer consider variants in the reasoning format. Prior works showed that different queries are better solved following different reasoning processes. In their work, the authors consider the most commonly adopted formats, i.e., (1) CoT: solving the question step-by-step in natural language, and (2) PoT: addressing the question through code generation.

Verification Layer Finally, the verification layer is responsible for checking the correctness of the proposed solution. It is particularly useful for problems where verification is significantly easier than solving the problem itself, e.g., the Game of 24. Therefore, the authors set a Self-Verification action module in this layer. If this module determines that the reasoning process from the solution layer is incorrect, the LLM will revert to the solution layer to reattempt to solve the problem. During this reattempt, the LLM is provided with both the initial answer and the feedback from the verifier explaining why the initial answer was incorrect. The process continues until the verifier confirms that the answer is correct or the pre-defined maximum number of iterations for self-verification is reached.

An overview of DOTS’s learning process is presented in Figure 2 below, consisting of three key steps: (i) Defining atomic reasoning modules, each of which represents a distinct reasoning action, (ii) Searching for optimal action trajectories, wherein various reasoning paths are explored and evaluated to identify optimal reasoning actions for questions in the training data, and (iii) Fine-tuning LLMs to plan for optimal reasoning trajectories. The atomic reasoning modules were described earlier. In terms of searching for optimal action trajectories, the authors teach the external/internalized planner to plan for the optimal reasoning trajectory by first constructing training data containing questions and their optimal action trajectories for the specific task-solving LLM. They obtain this by iteratively searching all possible reasoning trajectories for each question, including exploring the current paths and pruning paths that are unlikely to be optimal. The task-solving LLM is used during this search process to generate answers to make the reasoning trajectory align with their intrinsic ability to perform different reasoning actions effectively. An algorithm is provided in the paper, detailing the entire process formally.

Finally, having obtained the optimal trajectories, the authors use supervised fine-tuning with cross-entropy loss to train the planner LLM to predict optimal trajectories for input questions and the specific solver LLM. For external planner tuning, a lightweight LLM-p is trained to predict a concatenation of the explanation and the optimal trajectory; for internalized planner tuning, the solver LLMs is trained to predict the explanation, the optimal trajectory, the reasoning process collected from LLMs itself, and the true answer y*. Equations are provided in the paper for each of these steps for the interested reader.

Now on to experiments. The effectiveness of the proposed method is evaluated across multiple datasets and various reasoning tasks (Table 2 below). Based on the distribution of the training and testing data, the evaluation is divided into three settings: the in-distribution setting, which assesses the model's performance on data similar to what it encountered during training; the few-shot setting, which tests whether the method can learn effectively from a small amount of labeled data, acknowledging that it is often challenging to gather large amounts of in-domain training data in real-world scenarios; and the out-of-distribution (OOD) setting, which evaluates the model's ability to handle scenarios for which it was not explicitly trained, testing its generalization capabilities. The MATH training set is used for the training data.

Table 3 below presents the results of using the external planner, which suggest that:

External planner tuning outperforms other methods on the in-domain task. The DOTS method achieves 57.7% accuracy with Llama-3-70b-Instruct and 75.4% accuracy with GPT-4o-mini on MATH, achieving significant improvement than baselines. This suggests that it is is robust across different LLMs and it can significantly improve the LLM’s zero-shot reasoning ability. The improvement from DOTS remains consistent as the solver LLM’s capabilities increase, indicating DOTS’ potential long-term value even as LLMs continue to improve rapidly.

The external planner can learn the appropriate action trajectory with only a few training examples. On the BBH, DOTS achieves improvements of 3.5% and 3.1% over the best static methods when using Llama-3-70B-Instruct and GPT-4o-mini, respectively.

The authors also present some internalized planner tuning results, but I’ll skip these as the findings and improvements are consistent. Instead, of the many results presented, I wanted to focus on OOD tasks, as these are becoming increasingly important owing to a focus on responsible and trustworthy AI.

Impressively, as shown below, the authors’ method consistently generalizes well across diverse OOD challenges. Static methods often fluctuate significantly in performance (e.g., CoT showing a slight advantage on MMLU-Pro and StrategyQA over DOTS using the Llama-3-70B-Instruct model, but then experience a sharp decline on DeepMind Math). This pattern of fluctuations can be observed in other methods as well, where some excel on individual tasks but fail to maintain strong performance. In contrast, DOTS continues to deliver consistently high accuracy across various models and datasets. The stability of the method is attributed by the authors to its ability to dynamically select appropriate reasoning trajectories. Results from the ablation study in Table 6 similarly support these conclusions.

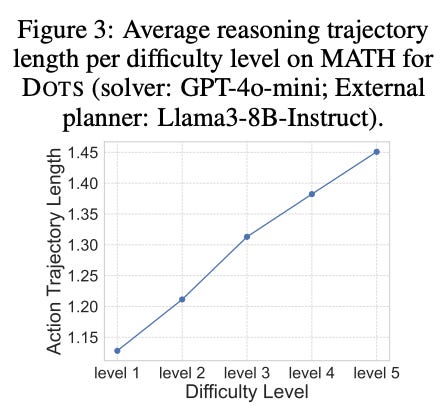
A musing I’ll add here is an interesting question the authors pose, but don’t go far enough in answering; namely, do we need more reasoning steps for difficult questions? Recent research suggests that LLMs can better solve difficult questions by increasing the thinking time in the inference stage. In their study, the authors do explore the relationship between question difficulty and the average reasoning action trajectory length (see below). The trajectory length is determined by assigning a value of 0 to the EMPTY module and 1 to all other actions, while the question difficulty is derived from annotated levels on the MATH dataset. The figure shows that harder problems demand more computational steps, resulting in longer reasoning trajectories. Case analyses further reveal that the DOTS planner increases the proportion of verification steps as problem difficulty rises. To quote the authors: “This highlights an exciting fact — LLMs can learn to employ more reasoning steps for challenging problems through exploration, without requiring explicit expert guidance.”

In closing, DOTS enables LLMs to autonomously think about appropriate reasoning actions before answering questions. By defining atomic reasoning action modules, searching for optimal action trajectories, and training LLMs to plan for reasoning questions, it is able to get LLMs to dynamically adapt to specific questions and their inherent capability. The flexibility of the two learning paradigms, i.e., external and internalized planner tuning, further emphasizes adaptability to different LLMs.