Musing 88: GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
Well-written and interesting paper out of Apple
Today’s paper: GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models. Mirzadeh et al. https://arxiv.org/pdf/2410.05229?
Any regular reader of this substack does not need me to state the obvious, although I will: Large Language Models (LLMs) have demonstrated remarkable capabilities across various domains, including natural language processing, question answering, and creative tasks. However, there is still a question on whether LLMs are capable of true logical reasoning. Some studies highlight impressive capabilities, but a closer examination reveals substantial limitations. There are suspicions around whether LLMs are really just doing a sophisticated kind of “probabilistic pattern-matching” as opposed to “formal reasoning.” Today’s paper offers a systematic way to study this issue.
The authors take on the task of mathematical reasoning at the grade-school level. Obviously, math reasoning is important for all kinds of problem-solving. The GSM8K (Grade School Math 8K) dataset has emerged as a popular benchmark for evaluating the mathematical reasoning capabilities of LLMs. It includes simple math questions with detailed solutions, making it suitable for techniques like Chain-of-Thought (CoT) prompting, but it provides only a single metric on a fixed set of questions. An example question is shown on the left-hand side of Figure 1 below.
What the authors are suggesting is to ‘generalize’ the dataset by deriving parsable templates from GSM8k, as shown on the right above. The result is GSM-Symbolic, a benchmark that generates diverse variants of GSM8K questions using symbolic templates.
The annotation process includes identifying variables, defining their domains, and establishing necessary conditions to ensure the correctness of both questions and answers. Given that the questions are at a grade-school level, a common condition is divisibility, ensuring answers are whole numbers. Common proper names (e.g., people, foods, currencies) are used to simplify template creation.
After template creation, several automated checks are performed to verify the annotation process. For instance, checks confirm that none of the original variable values appear in the template, that original values meet all conditions, and that the final answer matches the answer to the original question.
Once data are generated, 10 random samples per template undergo manual review. As a final automated step, after evaluating all models, it is verified that at least two models answer each question correctly; otherwise, the question is manually reviewed again.
Let’s jump to experiments. The authors report on more than 20 open models of various sizes, ranging from 2B to 27B. Additionally, they include state-of-the-art closed models such as GPT-4o-mini, GPT-4o, o1-mini, and o1-preview. The first set of results is shown above in Figure 2. By adjusting the domains of variables, the sample size and difficulty level can be modified. Notably, all models show significant variance across different sets. For example, the performance gap for the Gemma2-9B model between its worst and best outcomes exceeds 12%, while for the Phi-3.5-mini model, this gap is around 15%. This variation is noteworthy, given that the only differences across instances of each question are changes in names and values, while the core reasoning steps required to solve each question remain unchanged.
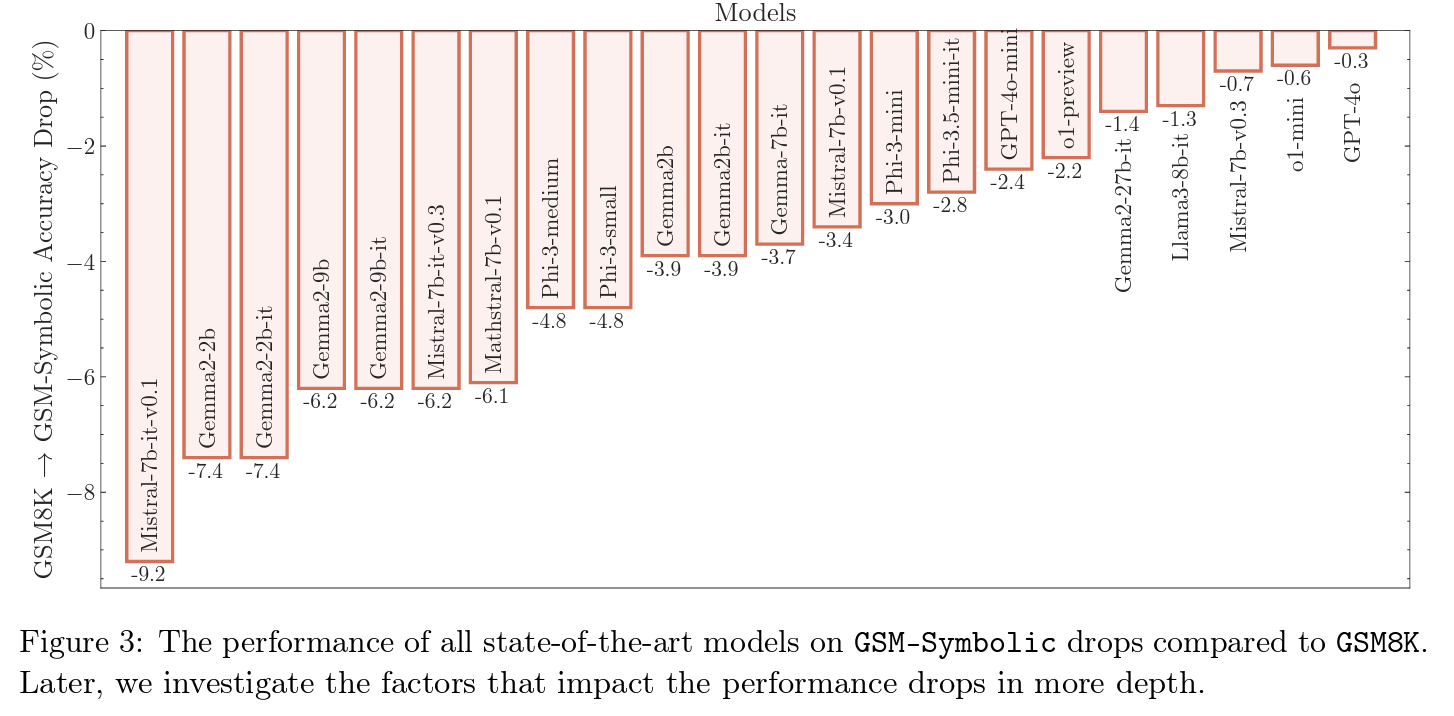
Below, the authors do a direct comparison of the models to assess by how much the performance drops on GSM-Symbolic compared to GSM8k. We can see that for models such as Gemma2-9B, Phi-3, Phi-3.5, and Mathstral-7B, the drop in performance is higher than for models such as Llama3-8b and GPT-4o. All of this shows that (math) reasoning abilities in LLMs is fragile.
But just how ‘fragile’ is math reasoning in LLMs? The authors first investigate the impact of the type of change to understand the difference between changing names (e.g., person names, places, foods, currencies, etc.) versus changing numbers (i.e., the values of variables). Figure 4 below illustrates that while performance variation remains, the variance is reduced when altering names compared to numbers. It is both notable and concerning that such performance variability occurs with only name changes, as this degree of fluctuation would be unexpected from a grade-school student with a solid mathematical understanding. In other words, as the difficulty of changes increases—from names to numbers—performance declines, and variance rises, overall suggesting that the reasoning abilities of state-of-the-art language models are fragile.
Next, the authors investigate how performance changes when they make the benchmark more ‘difficult’ by generating several new templates from the GSM-Symb, as illustrated below in Fig.5. First, they remove one clause, but then, they add one or two clauses to increase the difficulty. Importantly, the clauses here are ‘relevant’ in the sense that they are all necessary for correctly answering the question.
Without showing the curves, you can guess what the results were. The trend in the evolution of performance distribution is consistent across all models: as difficulty increases, performance declines, and variance grows. Notably, the overall rate of accuracy drop also accelerates as difficulty rises. This aligns with the hypothesis that models are not engaging in formal reasoning, as the number of required reasoning steps increases linearly, yet the drop rate appears steeper. Additionally, in light of the pattern-matching hypothesis, the increase in variance suggests that as difficulty escalates, models find it substantially harder to rely on searching and pattern-matching strategies.
Now the authors do something similar, but this time, they only add “seemingly relevant” statements that are actually irrelevant, as the figure above shows. Results are intriguing enough that I show it below. The figure is slightly complicated so let’s break it down a little.
NoOp-Symb (Using GSM-Symbolic shots of the same question): During evaluation, eight different versions of the same question from GSM-Symbolic are included. Each version provides the necessary reasoning steps. The target question from GSM-NoOp then presents another variation of the same question, differing only in values and including an inconsequential clause. This setup is intended to simplify the task by highlighting that the extra information in the target question is irrelevant. However, as shown in Fig. 8b, performance remains within the standard deviation, even with eight versions of the same question providing the reasoning chain. Interestingly, Fig. 8c reveals that some models can perform significantly better under this setup, despite not achieving comparable results on GSM8K and GSM-Symbolic, which we consider a noteworthy finding.
NoOp-NoOp (Using GSM-NoOp shots of different questions): In this setup, eight shots are provided, randomly selected from different GSM-NoOp questions. These questions share the feature that the correct answer should disregard the No-Op statement. For the Llama-3-8B model, we observe that performance remains unchanged compared to the original No-Op model, whereas for the Phi-3 model, performance shows a slight decrease.
The introduction of GSM-NoOp exposes a critical flaw in LLMs’ ability to genuinely understand mathematical concepts and discern relevant information for problem-solving. Adding seemingly relevant but ultimately inconsequential information to the logical reasoning of the problem led to substantial performance drops of up to 65% across all state-of-the-art models. Ultimately, the work underscores significant limitations in the ability of LLMs to perform genuine mathematical reasoning. The high variance in LLM performance on different versions of the same question, their substantial drop in performance with a minor increase in difficulty, and their sensitivity to inconsequential information indicate that their reasoning is fragile. It may resemble sophisticated pattern matching more than true logical reasoning.
To close out, it is worth remembering that both GSM8K and GSM-Symbolic are very simple: you can solve them if you just read them. You don’t need anything more than grade-school math. Only basic arithmetic and common sense is required. As the authors point out, it is likely that the limitations of these models will become even more pronounced in more challenging benchmarks. And this points to the significantly more work needed to understand the safety of these models.